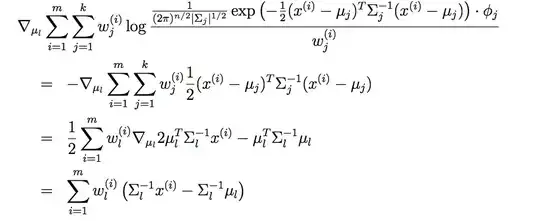Some plots to explore the data
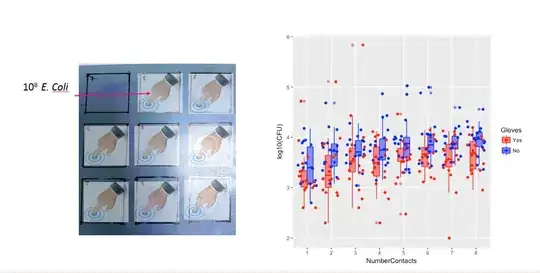
Below are eight, one for each number of surface contacts, x-y plots showing gloves versus no gloves.
Each individuals is plotted with a dot. The mean and variance and covariance are indicated with a red dot and the ellipse (Mahalanobis distance corresponding to 97.5% of the population).
You can see that the effects are only small in comparison to the spread of the population. The mean is higher for 'no gloves' and the mean changes a bit higher up for more surface contacts (which can be shown to be significant). But the effect is only little in size (overall a $\frac{1}{4}$ log reduction), and there are many individuals for who there is actually a higher bacteria count with the gloves.
The small correlation shows that there is indeed a random effect from the individuals (if there wasn't an effect from the person then there should be no correlation between the paired gloves and no gloves). But it is only a small effect and an individual may have different random effects for 'gloves' and 'no gloves' (e.g. for all different contact point the individual may have consistently higher/lower counts for 'gloves' than 'no gloves').
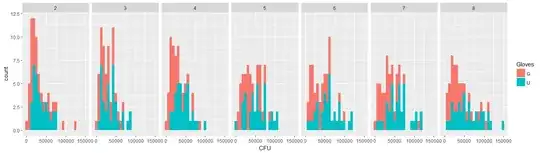
Below plot are separate plots for each of the 35 individuals. The idea of this plot is to see whether the behavior is homogeneous and also to see what kind of function seems suitable.
Note that the 'without gloves' is in red. In most of the cases the red line is higher, more bacteria for the cases 'without gloves'.
I believe that a linear plot should be sufficient to capture the trends here. The disadvantage of the quadratic plot is that the coefficients are gonna be more difficult to interpret (you are not gonna see directly whether the slope is positive or negative because both the linear term and the quadratic term have an influence on this).
But more importantly you see that the trends differ a lot among the different individuals and therefore it may be useful to add a random effect for not only the intercept, but also the slope of the individual.

Model
With the model below
- Each individual will get it's own curve fitted (random effects for linear coefficients).
- The model uses log-transformed data and fits with a regular (gaussian) linear model. In the comments amoeba mentioned that a log link is not relating to a lognormal distribution. But this is different. $y \sim N(\log(\mu),\sigma^2)$ is different from $\log(y) \sim N(\mu,\sigma^2)$
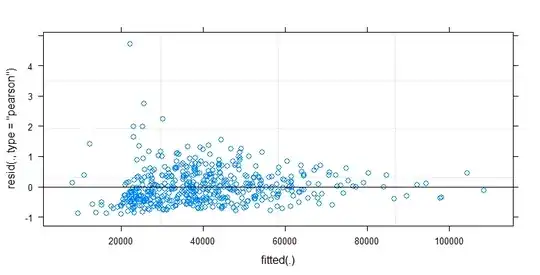
- Weights are applied because the data is heteroskedastic. The variation is more narrow towards the higher numbers. This is probably because the bacteria count has some ceiling and the variation is mostly due to failing transmission from the surface to the finger (= related to lower counts). See also in the 35 plots. There are mainly a few individuals for which the variation is much higher than the others. (we see also bigger tails, overdispersion, in the qq-plots)
- No intercept term is used and a 'contrast' term is added. This is done to make the coefficients easier to interpret.
.
K <- read.csv("~/Downloads/K.txt", sep="")
data <- K[K$Surface == 'P',]
Contactsnumber <- data$NumberContacts
Contactscontrast <- data$NumberContacts * (1-2*(data$Gloves == 'U'))
data <- cbind(data, Contactsnumber, Contactscontrast)
m <- lmer(log10CFU ~ 0 + Gloves + Contactsnumber + Contactscontrast +
(0 + Gloves + Contactsnumber + Contactscontrast|Participant) ,
data=data, weights = data$log10CFU)
This gives
> summary(m)
Linear mixed model fit by REML ['lmerMod']
Formula: log10CFU ~ 0 + Gloves + Contactsnumber + Contactscontrast + (0 +
Gloves + Contactsnumber + Contactscontrast | Participant)
Data: data
Weights: data$log10CFU
REML criterion at convergence: 180.8
Scaled residuals:
Min 1Q Median 3Q Max
-3.0972 -0.5141 0.0500 0.5448 5.1193
Random effects:
Groups Name Variance Std.Dev. Corr
Participant GlovesG 0.1242953 0.35256
GlovesU 0.0542441 0.23290 0.03
Contactsnumber 0.0007191 0.02682 -0.60 -0.13
Contactscontrast 0.0009701 0.03115 -0.70 0.49 0.51
Residual 0.2496486 0.49965
Number of obs: 560, groups: Participant, 35
Fixed effects:
Estimate Std. Error t value
GlovesG 4.203829 0.067646 62.14
GlovesU 4.363972 0.050226 86.89
Contactsnumber 0.043916 0.006308 6.96
Contactscontrast -0.007464 0.006854 -1.09

code to obtain plots
chemometrics::drawMahal function
# editted from chemometrics::drawMahal
drawelipse <- function (x, center, covariance, quantile = c(0.975, 0.75, 0.5,
0.25), m = 1000, lwdcrit = 1, ...)
{
me <- center
covm <- covariance
cov.svd <- svd(covm, nv = 0)
r <- cov.svd[["u"]] %*% diag(sqrt(cov.svd[["d"]]))
alphamd <- sqrt(qchisq(quantile, 2))
lalpha <- length(alphamd)
for (j in 1:lalpha) {
e1md <- cos(c(0:m)/m * 2 * pi) * alphamd[j]
e2md <- sin(c(0:m)/m * 2 * pi) * alphamd[j]
emd <- cbind(e1md, e2md)
ttmd <- t(r %*% t(emd)) + rep(1, m + 1) %o% me
# if (j == 1) {
# xmax <- max(c(x[, 1], ttmd[, 1]))
# xmin <- min(c(x[, 1], ttmd[, 1]))
# ymax <- max(c(x[, 2], ttmd[, 2]))
# ymin <- min(c(x[, 2], ttmd[, 2]))
# plot(x, xlim = c(xmin, xmax), ylim = c(ymin, ymax),
# ...)
# }
}
sdx <- sd(x[, 1])
sdy <- sd(x[, 2])
for (j in 2:lalpha) {
e1md <- cos(c(0:m)/m * 2 * pi) * alphamd[j]
e2md <- sin(c(0:m)/m * 2 * pi) * alphamd[j]
emd <- cbind(e1md, e2md)
ttmd <- t(r %*% t(emd)) + rep(1, m + 1) %o% me
# lines(ttmd[, 1], ttmd[, 2], type = "l", col = 2)
lines(ttmd[, 1], ttmd[, 2], type = "l", col = 1, lty=2) #
}
j <- 1
e1md <- cos(c(0:m)/m * 2 * pi) * alphamd[j]
e2md <- sin(c(0:m)/m * 2 * pi) * alphamd[j]
emd <- cbind(e1md, e2md)
ttmd <- t(r %*% t(emd)) + rep(1, m + 1) %o% me
# lines(ttmd[, 1], ttmd[, 2], type = "l", col = 1, lwd = lwdcrit)
invisible()
}
5 x 7 plot
#### getting data
K <- read.csv("~/Downloads/K.txt", sep="")
### plotting 35 individuals
par(mar=c(2.6,2.6,2.1,1.1))
layout(matrix(1:35,5))
for (i in 1:35) {
# selecting data with gloves for i-th participant
sel <- c(1:624)[(K$Participant==i) & (K$Surface == 'P') & (K$Gloves == 'G')]
# plot data
plot(K$NumberContacts[sel],log(K$CFU,10)[sel], col=1,
xlab="",ylab="",ylim=c(3,6))
# model and plot fit
m <- lm(log(K$CFU[sel],10) ~ K$NumberContacts[sel])
lines(K$NumberContacts[sel],predict(m), col=1)
# selecting data without gloves for i-th participant
sel <- c(1:624)[(K$Participant==i) & (K$Surface == 'P') & (K$Gloves == 'U')]
# plot data
points(K$NumberContacts[sel],log(K$CFU,10)[sel], col=2)
# model and plot fit
m <- lm(log(K$CFU[sel],10) ~ K$NumberContacts[sel])
lines(K$NumberContacts[sel],predict(m), col=2)
title(paste0("participant ",i))
}
2 x 4 plot
#### plotting 8 treatments (number of contacts)
par(mar=c(5.1,4.1,4.1,2.1))
layout(matrix(1:8,2,byrow=1))
for (i in c(1:8)) {
# plot canvas
plot(c(3,6),c(3,6), xlim = c(3,6), ylim = c(3,6), type="l", lty=2, xlab='gloves', ylab='no gloves')
# select points and plot
sel1 <- c(1:624)[(K$NumberContacts==i) & (K$Surface == 'P') & (K$Gloves == 'G')]
sel2 <- c(1:624)[(K$NumberContacts==i) & (K$Surface == 'P') & (K$Gloves == 'U')]
points(K$log10CFU[sel1],K$log10CFU[sel2])
title(paste0("contact ",i))
# plot mean
points(mean(K$log10CFU[sel1]),mean(K$log10CFU[sel2]),pch=21,col=1,bg=2)
# plot elipse for mahalanobis distance
dd <- cbind(K$log10CFU[sel1],K$log10CFU[sel2])
drawelipse(dd,center=apply(dd,2,mean),
covariance=cov(dd),
quantile=0.975,col="blue",
xlim = c(3,6), ylim = c(3,6), type="l", lty=2, xlab='gloves', ylab='no gloves')
}