The webpage that you link provides the answer, near the bottom, in a note dated 11 Feb 2016:
The old trendline was a third order polynomial trendline. It worked fine for 0-120,000 km where there are lots of entries but after there were no more entries it showed a sharp drop. The new trendline is polynomial until the data ends but linear afterwards.
It's not clear what is meant by "until the data ends", but that type of plot (nonlinear to start, linear at an extreme) seems to be pretty consistent with the trend line pictured. Other text on that page specifies that a linear trend is assumed at high mileage: "The red fitted line has a slope above 60.000 km (say 40,000 miles) of 1% per 50.000 km (30,000 miles)."
That's not an unusual way to proceed. As another example, restricted cubic splines fit nonlinear relationships for most of the data, but enforce linear relationships for data points near the extremes.
So there is no theoretical basis for the shape of the relationship, it's just a fit of an arbitrary curve to the data.
Finally, plots like this, with the lower y-axis limit far from 0, can be misleading. Note that the value of the trend line even near 200,000 miles is still 90% of capacity. The web page also shows a plot with the y-axis lower limit at 0, which is perhaps more enlightening. Data are consistent with some early loss followed by a slow linear decline.
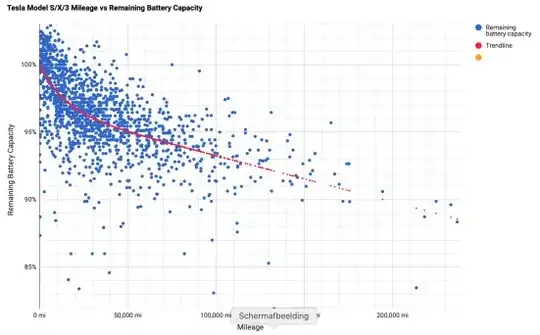 Source: link
Source: link