Random process not so random after all (deterministic)

Question

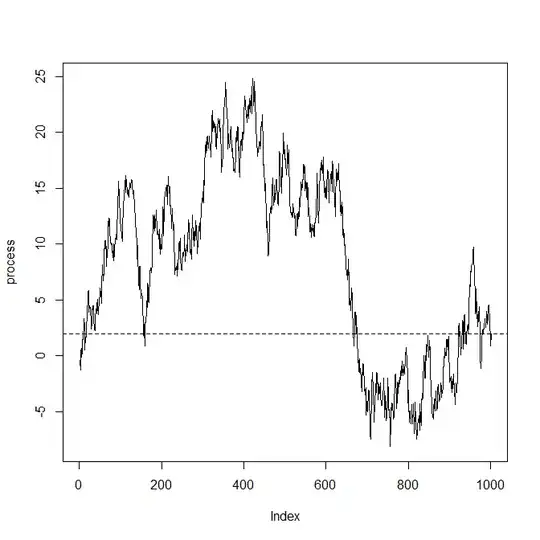
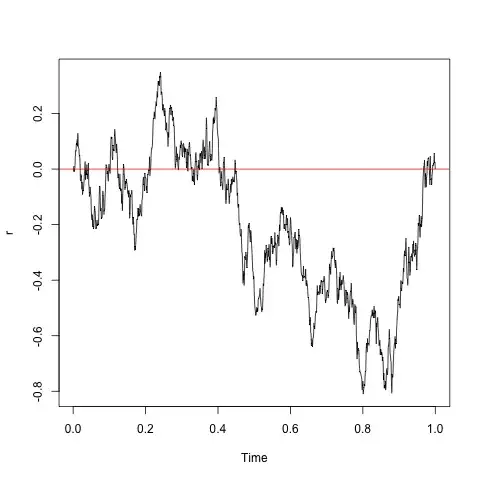
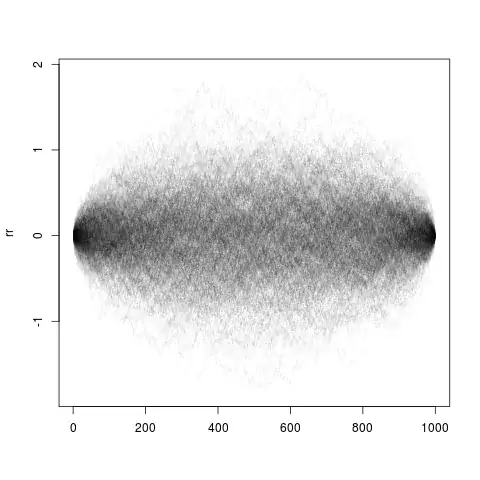
I would like to show (demonstrate by simulation) a random process that turns out after $i$ interactions to be deterministic, i.e. ends at predefined value (roughly) known at time $t=1$.

Conditions for the solution:

1) The random process should display randomness visible (graph) = interactive

2) The "convergence" to the end result should be gradual and therefore the end result surprising to the observer.

3) Solution in R (hopefully).

The meaning of surprising in this case: I mean, during the generating process, the observer expectation is not (rational?) .... (Surprise in sense of conviction that random is not random after all).

Sub-question (setup):

Does it matter whether the terminal (final) value is revealed to observer a priori (at the beginning of the generating process series) or after the process ends (to confirm the values match)?

Summary:

1) If solution is not provided, how to approach it? (any hint helps)

2) Which tool (statistical/modeling) should be used? How to set up the process?

EDIT: improved version (of what I'm asking)

Simulate a (large) number of identically distributed but dependent random variables, such that their sum is ideally equal to a prespecified value, or failing that (for continuous RVs, we will hit a single number with probability 0), which is in a given range with a given probability. (with @Stephan kind help.)

Answer 1

Suppose that after $T$ iterations, your process should end up at a predefined value $m$.

You can first simulate a process $f_t$ with whatever characteristics you want and then modify it as follows:

$$ f_t \mapsto f_t + \frac{t}{T}(m-f_T) $$

Note that this requires that we know the end value $f_T$ of the unconstrained process when we modify it at time $t$.

Here is an example with $T=1000$ and $m=2$:

target <- 2
n_steps <- 1000

set.seed(1)
process_raw <- cumsum(rnorm(n_steps+1))
process <- process_raw + (0:n_steps)/n_steps * (target-tail(process_raw,1))

plot(process,type="l")
abline(h=target,lty=2)

If you need something that can be calculated at time $t$ without "looking ahead", you can use $f_t$ instead of $f_T$ in the above formula.

$$ f_t \mapsto f_t + \frac{t}{T}(m-f_t) $$

However, then your process will have lower and lower variance as $t\to T$:

process <- process_raw + (0:n_steps)/n_steps * (target-process_raw)

plot(process,type="l")
abline(h=target,lty=2)

Answer 2

What you are asking for is called a Brownian bridge ; there is an answer elsewhere on CV that asks how to convert a Brownian bridge into a Brownian "excursion": Simulating a Brownian Excursion using a Brownian Bridge? . That question uses the rbridge() function from the e1071 package:

library(e1071)
set.seed(101)
r <- rbridge()  ## default: end time=1, frequency=1000
plot(r)
abline(h=0,col="red")

The underlying code for rbridge is pretty simple:

z <- rwiener(end = end, frequency = frequency)
ts(z - time(z) * as.vector(z)[frequency], start = 1/frequency, 
    frequency = frequency)

Stripped of its extra details, this corresponds to $B(t) = W(t) - t/T \cdot W(T)$, where $W$ is a Wiener process and $T$ is the ending time, as suggested in the Wikipedia article.

This simulates a Brownian bridge that starts and ends at zero; I would suggest adding a linear trend if you want to modify the starting and ending points (as suggested by the "general case" section of the Wikipedia article).

An ensemble:

rr <- replicate(500,rbridge())
matplot(rr,type="l",col=adjustcolor("black",alpha=0.05))

A comment on a previous version of this answer argued that the volatility would not be constant; based on a numerical experiment (easier than thinking), I believe this is false - the volatility is constant (we can also see this by looking at the $B(t)$ expression above ...

However, a careful observer should be able to detect that something is going on, because $\Delta x$ will be biased toward the starting point (similar to, but not the same as, an Ornstein-Uhlenbeck process).