I would like to simulate a Brownian excursion process (a Brownian motion that is conditioned always be positive when $0 \lt t \lt 1$ to $0$ at $t=1$). Since a Brownian excursion process is a Brownian bridge that is conditioned to always be positive, I was hoping to simulate the motion of a Brownian excursion using a Brownian bridge.
In R, I am using thh 'e1017' package to simulate a Brownian bridge process. How can I use this Brownian bridge process to create a Brownian excursion?
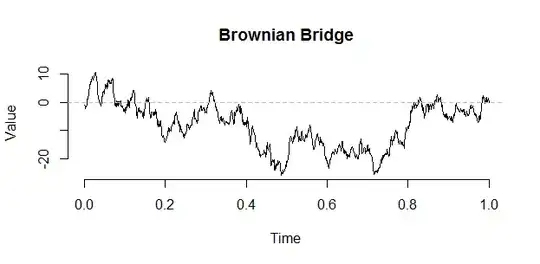
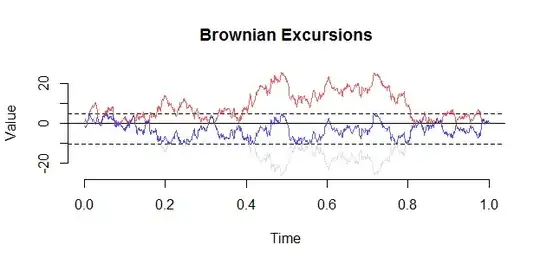
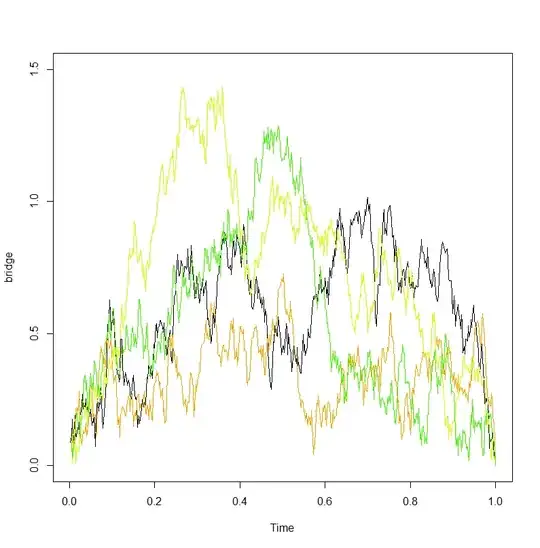
A Brownian excursion can be constructed from a bridge using the following construction by Vervaat: https://projecteuclid.org/download/pdf_1/euclid.aop/1176995155
A quick approximation in R, using @whuber's BB code, is
n <- 1001
times <- seq(0, 1, length.out=n)
set.seed(17)
dW <- rnorm(n)/sqrt(n)
W <- cumsum(dW)
# plot(times,W,type="l") # original BM
B <- W - times * W[n] # The Brownian bridge from (0,0) to (1,target)
# plot(times,B,type="l")
# Vervaat construction
Bmin <- min(B)
tmin <- which(B == Bmin)
newtimes <- (times[tmin] + times) %% 1
J<-floor(newtimes * n)
BE <- B[J] - Bmin
plot(1:length(BE)/n,BE,type="l")
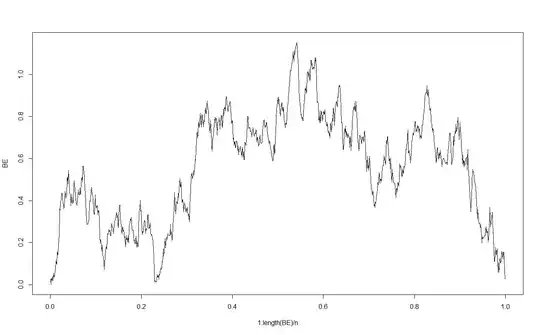
Here is another plot (from set.seed(21)). A key observation with an excursion is that the conditioning actually manifests as a "repulsion" from 0, and you are unlikely to see an excursion come close to $0$ on the interior of $(0,1)$.
Aside: The distribution of the absolute value of a Brownian bridge $(|BB_t|)_{0 \le t \le 1}$ and the excursion, $(BB_t)_{0 \le t \le 1}$ conditioned to be positive, are not the same. Intuitively, the excursion is repelled from the origin, because Brownian paths coming too close to the origin are likely to go negative soon after and thus are penalised by the conditioning.
This can even be illustrated with a simple random walk bridge and excursion on $6$ steps, which is a natural discrete analogue of BM (and converges to BM as steps becomes large and you rescale).
Indeed, take an symmetric SRW starting from $0$. First, let us consider the "bridge" conditioning and see what happens if we just take the absolute value. Consider all simple paths $s$ of length $6$ that start and end at $0$. The number of such paths is ${6 \choose 3} = 20$. There are $2\times {4 \choose 2} = 12$ of these for which $|s_2| = 0$. In other words, the probability for the absolute value of our SRW "bridge" (conditioned to end at $0$) to have value 0 at step $2$ is $12/20 = 0.6$.
Secondly, we will consider the "excursion" conditioning. The number of non-negative simple paths $s$ of length $6 = 2*3$ that end at $0$ is the Catalan number $C_{m=3} = {2m\choose m}/(m+1) = 5$. Exactly $2$ of these paths have $s_2 = 0$. Thus, the probability for our SRW "excursion" (conditioned to stay positive and end at $0$) to have value 0 at step $2$ is $2/5 = 0.4 < 0.6$.
In case you still doubt this phenomenon persists in the limit you could consider the probability for SRW bridges and excursions of length $4n$ hitting 0 at step $2n$.
For the SRW excursion: we have $$\mathbb{P}(S_{2n} = 0 | S_{j} \ge 0, j \le 4n, S_{4n} = 0) = C_n^2 / C_{2n} \sim (4^{2n}/\pi n^3)/(4^{2n} / \sqrt{(2n)^3 \pi})$$ using the aysmptotics from wikipedia https://en.wikipedia.org/wiki/Catalan_number. I.e. it is like $cn^{-3/2}$ eventually.
For abs(SRW bridge): $$\mathbb{P}(|S_{2n}| = 0 | S_{4n} = 0) = {2n \choose n}^2 / {4n \choose 2n} \sim (4^n/\sqrt{\pi n})^2/(4^{2n} / \sqrt{2n\pi})$$ using the asymptotics from wikipedia https://en.wikipedia.org/wiki/Binomial_coefficient. This is like $cn^{-1/2}$.
In other words, the asymptotic probability to see the SRW bridge conditioned to be positive at $0$ near the middle is much smaller than that for the absolute value of the bridge.
Here is an alternative construction based on a 3D Bessel process instead of a Brownian bridge. I use the facts explained in https://projecteuclid.org/download/pdf_1/euclid.ejp/1457125524
Overview- 1) Simulate a 3d Bessel process. This is like a BM conditioned to be positive. 2) Apply an appropriate time-space rescaling in order to obtain a Bessel 3 bridge (Equation (2) in the paper). 3) Use the fact (noted just after Theorem 1 in the paper) that a Bessel 3 bridge actually has the same distribution as a Brownian excursion.
A slight drawback is that you need to run the Bessel process for quite a while (T=100 below) on a relatively fine grid in order for the space/time scaling to kick in at the end.
## Another construction of Brownian excursion via Bessel processes
set.seed(27092017)
## The Bessel process must run for a long time in order to construct a bridge
T <- 100
n <- 100001
d<-3 # dimension for Bessel process
dW <- matrix(ncol = n, nrow = d, data=rnorm(d*n)/sqrt(n/T))
dW[,1] <- 0
W <- apply(dW, 1, cumsum)
BessD <- apply(W,1,function(x) {sqrt(sum(x^2))})
times <- seq(0, T, length.out=n)
# plot(times,BessD, type="l") # Bessel D process
times01 <- times[times < 1]
rescaletimes <- pmin(times01/(1-times01),T)
# plot(times01,rescaletimes,type="l") # compare rescaled times
# create new time index
rescaletimeindex <- sapply(rescaletimes,function(x){max(which(times<=x))} )
BE <- (1 - times01) * BessD[rescaletimeindex]
plot(times01,BE, type="l")
Here is the output:
The Reflection Principle asserts
if the path of a Wiener process $f(t)$ reaches a value $f(s) = a$ at time $t = s$, then the subsequent path after time $s$ has the same distribution as the reflection of the subsequent path about the value $a$
Wikipedia, accessed 9/26/2017.
Accordingly we may simulate a Brownian bridge and reflect it about the value $a=0$ simply by taking its absolute value. The Brownian bridge is simulated by subtracting the trend from the start point $(0,0)$ to the end $(T,B(T))$ from the Brownian motion $B$ itself. (Without any loss of generality we may measure time in units that make $T=1$. Thus, at time $t$ simply subtract $B(T)t$ from $B(t)$.)
The same procedure may be applied to display a Brownian motion conditional not only on returning to a specified value at time $T\gt 0$ (the value is $0$ for the bridge), but also on remaining between two limits (which necessarily include the starting value of $0$ at time $0$ and the specified ending value).
This Brownian motion starts and ends with a value of zero: it is a Brownian Bridge.
The red graph is a Brownian excursion developed from the preceding Brownian bridge: all its values are nonnegative. The blue graph has been developed in the same way by reflecting the Brownian bridge between the dotted lines every time it encounters them. The gray graph displays the original Brownian bridge.
The calculations are simple and fast: divide the set of times into small intervals, generate independent identically distributed Normal increments for each interval, accumulate them, subtract the trend, and perform any reflections needed.
Here is R code. In it, W is the original Brownian motion, B is the Brownian bridge, and B2 is the excursion constrained between two specified values ymin (non-positive) and ymax (non-negative). Its technique for performing reflection using the modulus %% operator and componentwise minimum pmin may be of practical interest.
#
# Brownian bridge in n steps from t=0 to t=1.
#
n <- 1001
times <- seq(0, 1, length.out=n)
target <- 0 # Constraint at time=1
set.seed(17)
dW <- rnorm(n)
W <- cumsum(dW)
B <- W + times * (target - W[n]) # The Brownian bridge from (0,0) to (1,target)
#
# The constrained excursion.
#
ymax <- max(abs(B))/5 # A nice limit for illustration
ymin <- -ymax * 2 # Another nice limit
yrange2 <- 2*(ymax - ymin)
B2 <- (B - ymin) %% yrange2
B2 <- pmin(B2, yrange2-B2) + ymin
You could use a rejection method: simulate Brownian bridges and keep the positive ones. It works.
But. It is very slow, as a lot of sample trajectories are rejected. And the larger "frequency" you set, the less likely you are to find trajectories.
succeeded <- FALSE
while(!succeeded)
{
bridge <- rbridge(end = 1, frequency = 500)
succeeded=all(bridge>=0)
}
plot(bridge)
You can speed it up keeping the negative trajectories as well.
while(!succeeded)
{
bridge <- rbridge(end = 1, frequency = 500)
succeeded=all(bridge>=0)||all(bridge<=0)
}
bridge = abs(bridge)
plot(bridge)
