6

I need to generate random numbers from Beta distribution using random variables from Uniform distribution.
If I have two random variables $Y_1=U_1^{1/\alpha}$ and $Y_2=U_1^{1/\beta}$,
and If $Y_1+Y_2<= 1$ then $X=Y_1/(Y_1+Y_2)$ is from Beta distribution with parameters $\alpha\ and\ \beta$.

This is what I've done so far:
I've generated 10,000 random variables from a Uniform distribution.
I then used those rv to generate $Y_1 and\ Y_2 $ using $Y_1=U_1^{1/\alpha}$ and $Y_2=U_1^{1/\beta}$.
Then I generated $X$ using the formula $X=Y_1/(Y_1+Y_2)$.

Here is the R code I used:

library(dplyr)
# my plot
alpha <- 2
beta <- 4

set.seed(10)
u <- runif(10000,0,1)

y1 <- u^(1/alpha)
y2 <- u^(1/beta)


x <- data.frame(y1,y2 ) %>% 
  filter(y1+y2<=1) %>% # check that y1+y1 <=1
  mutate(x = y1/(y1+y2)) %>% # generate x random variable
  select(x) 

# plot x
hist(x$x)

# plot from beta distribution
hist(rbeta(10000,shape = 2,shape2 =4))

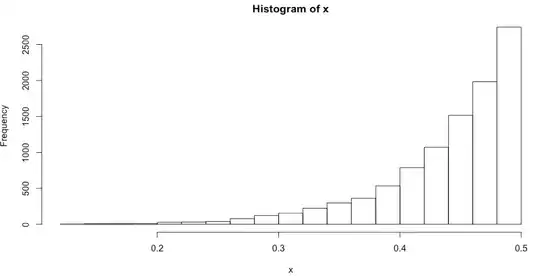
But when I plot this, the histogram seems to be going in the opposite direction to when I just generate rv from Beta distribution. Here is my plot: enter image description here

And here is the plot if I generate rv from actual beta distribution:
enter image description here

Why does my curve look different to the one from Beta distribution?
This question seems very similar, but the solution uses qbeta() function. I think I need to use my $X=Y_1/(Y_1+Y_2)$

jmich738
  • 271
  • 1
  • 3
  • 10
  • 3
    Hint: You need the $Y_i$ to be *independent.* – whuber May 26 '18 at 10:53
  • 5
    I believe it is a bit rude to downvote this question. The question is well explained and developed. The answer may be simple, but, it is a minor mistake anyone of us can do. – Jon Nagra May 27 '18 at 17:33
  • 3
    @whuber I think I got it. I generated only 1 sample from the Uniform distribution, where as I need to get generate 2 If I change my code to this, it looks like it's working: `y1 – jmich738 May 28 '18 at 09:40

1 Answers1

1

I just had the same problem with the distribution creation, thanks for the latest reply to the original post. Please find below a viable solution to create one RV in Python:

def beta(a,b):
    rv1 = np.random.rand()**(1/a)
    rv2 = np.random.rand()**(1/b)

    while (rv1+rv2) > 1:
        rv1 = np.random.rand()**(1/a)
        rv2 = np.random.rand()**(1/b)

    return = rv1 / (rv1+rv2)
Guenter
  • 111
  • 3
  • 1
    The code would crash on `u1+u2` since the variables are not defined. – Tim Jul 16 '21 at 11:46
  • copy paste error, apologies. It is rv1 and rv2 of course, thanks for pointing it out and the immediate downvote. – Guenter Jul 17 '21 at 10:45
  • What is the point of the `while` loop?? As far as I can tell, all it does is slow down the algorithm by an arbitrarily large factor. – whuber Jul 21 '21 at 15:46
  • I haven't found a proper explanation for this, but when testing this without the condition in the loop, the results are not following the beta distribution. I tested the results versus the distribution given a grid of input variables. – Guenter Jul 22 '21 at 22:05