2

I can generate as many samples from one or more uniform distribution (0,1) as I wish. How can I use this to generate a beta distribution ?

Xi'an
  • 90,397
  • 9
  • 157
  • 575
Malice
  • 163
  • 1
  • 6
  • 6
    A good place to start looking for answers to questions of this form ("how do I generate a random variable from a named distribution") is to search for encyclopedia entries about the distribution: typically, they will include information about random generation of values. The [Wikipedia article on the Beta distribution](https://en.wikipedia.org/wiki/Beta_distribution#Generating_beta-distributed_random_variates) is characteristic. – whuber Aug 29 '15 at 16:16
  • 2
    Luc Devroye discusses methods for this in his book; look it up there (and his book is free to download, too!) – J. M. is not a statistician Aug 30 '15 at 01:06
  • 1
    The book @Guesswhoitis means is at Luc's pages [here](http://luc.devroye.org/rnbookindex.html) – Glen_b Aug 30 '15 at 02:01

2 Answers2

6

I will use [R] not so much as a practical answer (rbeta would do the trick), but as an attempt at thinking through the probability integral transform. I hope you are familiar with the code so you can follow, or replicate (if this answers your question).

The idea behind the Probability Integral Transform is that since a $cdf$ monotonically increases in value from $0$ to $1$, applying the $cdf$ function to random values form whichever distribution we may be interested in will on aggregate generate as many results say, between $0.1$ and $0.2$ as from $0.8$ to $0.9$. Now, this is exactly what a $pdf$ of a $U(0,1)$. It follows that if we start with values from a random uniform, $U \sim (0,1)$ instead, and we apply the inverse $cdf$ of the distribution we are aiming at, we'll end up with random values of that distribution.

Let's quickly show it with the queen of the distributions... The Normal $N(0,1)$. We generate $10,000$ random values, and plug them into the $erf$ function, plotting the results:

# Random variable from a normal distribution:
x <- rnorm(1e4)
par(mfrow=c(1,2))
hist(x, col='skyblue', main = "Random Normal")

# When transform by obtaining the cdf (x) will give us a Uniform:
y <- pnorm(x)
hist(y, col='skyblue', main = "CDF(X)")

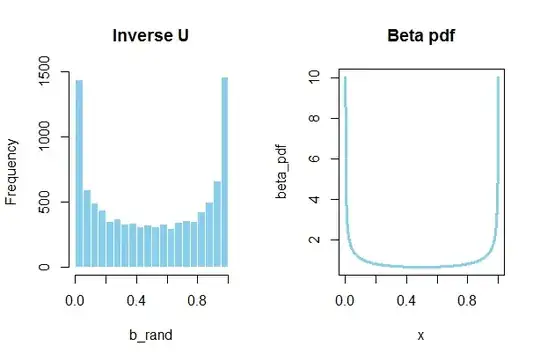
enter image description here

In your case, we are aiming for $X \sim Beta(\alpha, \beta)$. So let's get started at the end and come up with $10,000$ random values from a $U(0,1)$. We also have to select values for the shape parameters of the $Beta$ distribution. We are not constrained there, so we can select for example, $\alpha=0.5$ and $\beta=0.5$. Now we are ready for the inverse, which is simply the qbeta function:

U <- runif(1e4)
alpha <- 0.5
beta <- 0.5
b_rand <- qbeta(U, alpha, beta)
hist(b_rand, col="skyblue", main = "Inverse U")

Compare this to the shape of the $Beta(\alpha,\beta)$ $pdf$:

x <- seq(0, 1, 0.001)
beta_pdf <- dbeta(x, alpha, beta)
plot(beta_pdf, type ="l", col='skyblue', lwd = 3,
     main = "Beta pdf")

enter image description here

Antoni Parellada
  • 23,430
  • 15
  • 100
  • 197
  • 1
    Nice illustration (+1), but another reason it's impractical may be that the beta quantile function has to be approximated numerically & I'd bet rejection methods are quicker (because `rbeta` uses one). – Scortchi - Reinstate Monica Sep 01 '15 at 16:23
  • 2
    @Scortchi Hi there! Thanks for commenting. The post was intended (as all my posts, really) to kind of walk myself through the concepts. The hope is that may be someone else is also wresting with a basic understanding of the idea. There is no intention to provide a method. In any event, please feel free to improve the post by editing. Cheers! – Antoni Parellada Sep 01 '15 at 16:28
  • 1
    Oh yes, I got that - just thought it might be useful to mention a reason why you don't *always* use the probability integral transform in practice: the quantile function isn't always very easy to evaluate. – Scortchi - Reinstate Monica Sep 01 '15 at 16:38
  • 2
    I believe the point of the original question may have been to help the student understand the connection between Beta distributions and order statistics of the uniform distribution. – whuber Nov 02 '15 at 16:21
  • 4
    @whuber It's easy to agree with you, but that's how I interpreted it; not as a computational issue. As a student myself, working on the answer helped me go over this concept again - why is the "boring" uniform actually so interesting. – Antoni Parellada Nov 02 '15 at 16:24
  • @whuber: the issue with Uniform order statistics is that the parameters of the Beta distribution are then integers. – Xi'an Nov 04 '15 at 14:24
  • @Xi'an That's right, so it's not fully general. It's not even efficient except for small values of those parameters. Although we could get more creative--there are many possible solutions--[it's hard to know where to stop](http://stats.stackexchange.com/a/117711/919). :-) – whuber Nov 04 '15 at 18:44
2

You could use the inverse transform sampling method, which is useful to know about because it's a very general method that is not limited solely to the beta distribution.

Sycorax
  • 76,417
  • 20
  • 189
  • 313