How can I generate random floating-point numbers, the probability function of which is linear? Suppose I can generate uniform randoms.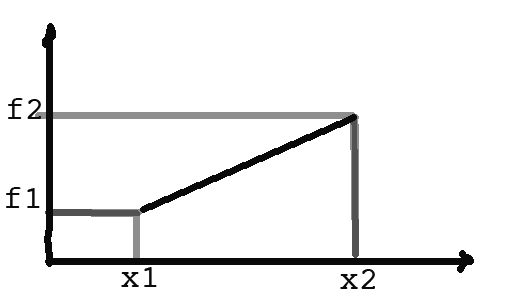
Plot is example of linear distribution. f - probability density, x - random value.
How can I generate random floating-point numbers, the probability function of which is linear? Suppose I can generate uniform randoms.
Plot is example of linear distribution. f - probability density, x - random value.
There are many methods. Here are a few.
You could use rejection ("accept-reject") with a uniform envelope.
could could use the inverse cdf method on the density, by working out the cdf and inverting it $X=F^{-1}(U)$
You could split into a uniform and a triangular part (i.e. a finite mixture of the two). The triangular part can be generated in any of several ways (e.g. the $\max$ of two uniforms, or using the inverse cdf method, ...) and then scaled to the right interval, and the uniform is trivial (simply scaled to the right interval).
if $x_1$ is positive, you could treat as triangular on $(0,x_2)$ and then use rejection in the case where it's below $x_1$. This will work pretty well if $x_1/x_2$ is small (a good bit less than half, say).
you could use the ziggurat method.
There are a number of other approaches. The choice between them would depend on considerations such as how much convenience vs speed matters (if you only need a few thousand values, speed probably doesn't matter much; if you need to use it many many times with potentially long runs, there it may matter much more).
This reminds me of another post about a linear pdf which had functional form:
$$ h(x) = \frac{1+\alpha x}{2}, \quad \quad x \in [-1,1], \quad \alpha\in[-1,1] $$
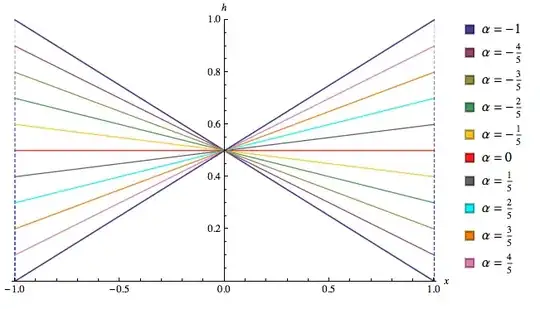
(source: tri.org.au)
I called this an 'acute linear' distribution, or a cute linear distribution.
If $X_1\sim \text{Triangular}(-1,1,1)$ and $X_2\sim \text{Uniform}(-1,1)$ are independent, then $$X\sim \alpha X_1+(1-\alpha ) X_2$$ ... has a cute Linear distribution.
Pseudo-random number generation
The cdf (within the domain of support) is: $$H = \frac{1}{4} (x+1) (\alpha (x-1)+2)$$
The inverse cdf is: $$x = H^{-1}(u) = \frac{\sqrt{\alpha ^2-2 \alpha +4 \alpha u+1}-1}{\alpha }$$
Replacing $u$ with a pseudo-random drawing from $\text{Uniform}(0,1)$ then yields a pseudo-random drawing from the above cute linear pdf $h(x)$.
If you wish to change the scale, or shift it, you can transform the data $X_{data}$ you generate .. e.g. $Y = b + c X_{data}$ ... which should be able to generate the richness of whatever structure you desire (might require a little bit of playing around, depending on what you are holding fixed).