I'm analyzing a certain dataset, and I need to understand how to choose the best model that fits my data. I'm using R.
An example of data I have is the following:
corr <- c(0, 0, 10, 50, 70, 100, 100, 100, 90, 100, 100)
These numbers correspond to the percentage of correct answers, under 11 different conditions (cnt):
cnt <- c(0, 82, 163, 242, 318, 390, 458, 521, 578, 628, 673)
Firstly I tried to fit a probit model, and a logit model. Just now I found in the literature another equation to fit data similar to mine, so I tried to fit my data, using the nls function, according to that equation (but I don't agree with that, and the author does not explain why he used that equation).
Here is the code for the three models I get:
resp.mat <- as.matrix(cbind(corr/10, (100-corr)/10))
ddprob.glm1 <- glm(resp.mat ~ cnt, family = binomial(link = "logit"))
ddprob.glm2 <- glm(resp.mat ~ cnt, family = binomial(link = "probit"))
ddprob.nls <- nls(corr ~ 100 / (1 + exp(k*(AMP-cnt))), start=list(k=0.01, AMP=5))
Now I plotted data and the three fitted curves:
pcnt <- seq(min(cnt), max(cnt), len = max(cnt)-min(cnt))
pred.glm1 <- predict(ddprob.glm1, data.frame(cnt = pcnt), type = "response", se.fit=T)
pred.glm2 <- predict(ddprob.glm2, data.frame(cnt = pcnt), type = "response", se.fit=T)
pred.nls <- predict(ddprob.nls, data.frame(cnt = pcnt), type = "response", se.fit=T)
plot(cnt, corr, xlim=c(0,673), ylim = c(0, 100), cex=1.5)
lines(pcnt, pred.nls, lwd = 2, lty=1, col="red", xlim=c(0,673))
lines(pcnt, pred.glm2$fit*100, lwd = 2, lty=1, col="black", xlim=c(0,673)) #$
lines(pcnt, pred.glm1$fit*100, lwd = 2, lty=1, col="green", xlim=c(0,673))
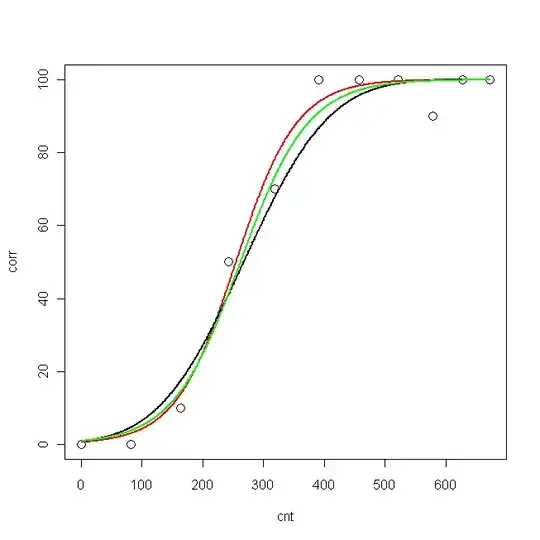
Now, I would like to know: what is the best model for my data?
- probit
- logit
- nls
The logLik for the three models are:
> logLik(ddprob.nls)
'log Lik.' -33.15399 (df=3)
> logLik(ddprob.glm1)
'log Lik.' -9.193351 (df=2)
> logLik(ddprob.glm2)
'log Lik.' -10.32332 (df=2)
Is the logLik sufficient to choose the best model? (It would be the logit-model, right?) Or is there something else I need to calculate?