Which independent variables are most important in predicting the response variable?

Question

I'm a biologist, and I have a large dataset that I'm trying to analyze. Here are the variables I'm working with:

• levels of 211 different metabolites in 16 different blood samples (predictor variables)
• how well each of the 16 blood samples performed in a specific test (response variable)

I am trying to figure out which variable(s) are the most important in predicting the performance of a blood sample in the test.

I would like to make these data more manageable by doing a PCA, but I'm new to this sort of analysis. I understand that a PCA will create groups of principal components (it will group metabolites that covary with each other and label each of these groups a principal component), but I'm not sure how to take into account the response variable in this analysis.

Any help would be much appreciated!!! Thank you.

> summary(metabolites_princomp)
Importance of components:
                          Comp.1     Comp.2      Comp.3      Comp.4
Standard deviation     3.9608225 0.40128486 0.259868774 0.215004349
Proportion of Variance 0.9805072 0.01006435 0.004220736 0.002889179
Cumulative Proportion  0.9805072 0.99057153 0.994792267 0.997681446
[...]

Answer 1

First, note that your understanding of PCA is slightly off. PCA doesn't "group" variables into principal components. Each principal component is, rather, a new variable (a "new metabolite") of the same length as each of your original variables (in your case, 16).

It's true that each principal component can represent a group of original metabolites, but it's more complicated and sophisticated than that. Each metabolite can actually be correlated with multiple principal components, each a different amount. It could be true that a group of metabolites are purely represented principal component A and another group is purely represented by principal component B, but it is far more likely that each is correlated with multiple PCs, each to a different extent.

So think of each PC as a new metabolite (in PCA parlance we'd call it an "eigenmetabolite") that is representative of a general pattern across the metabolites. Some metabolites are highly representative of this pattern, while some aren't, and some share some properties with multiple patterns.

Now we come to your question. The way we bring in a response variable is to look at the relationship- for example, a correlation or linear regression- between each principal component (each eigenmetabolite) and the response variable. Here is a neat little example in R code. (Note that I use the svd function rather than the pls package, as you might be using).

set.seed(1337)

center.rows = function(m) t(apply(m, 1, function(r) r - mean(r)))

response.var = rnorm(16, 0, 1)

relevant.metabolites = t(replicate(50, rnorm(16, response.var, 2)))
unrelated.metabolites = t(replicate(110, rnorm(16, 0, 2)))
metabolite.data = rbind(relevant.metabolites, unrelated.metabolites)

s = svd(center.rows(metabolite.data))

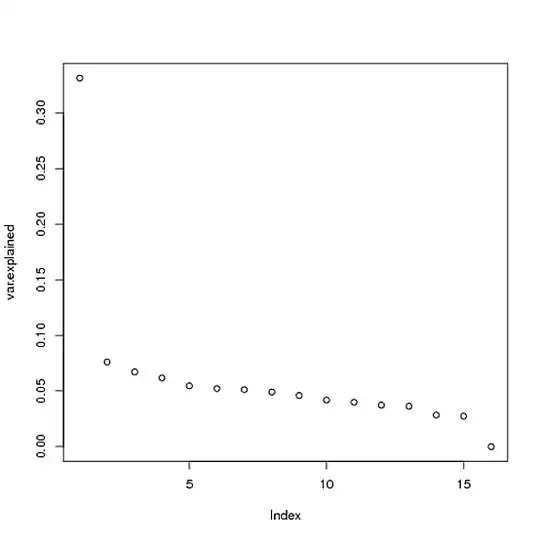
What I did is create a matrix of simulated metabolite data with 50 genes that are somewhat correlated with the response variable, and 110 genes that aren't. We can see that only one PC is significant, and it explains ~33% of the variance:

var.explained = s$d^2 / sum(s$d^2)
plot(var.explained)

Now let's compare that PC to the response variable:

plot(response.var, s$v[, 1])

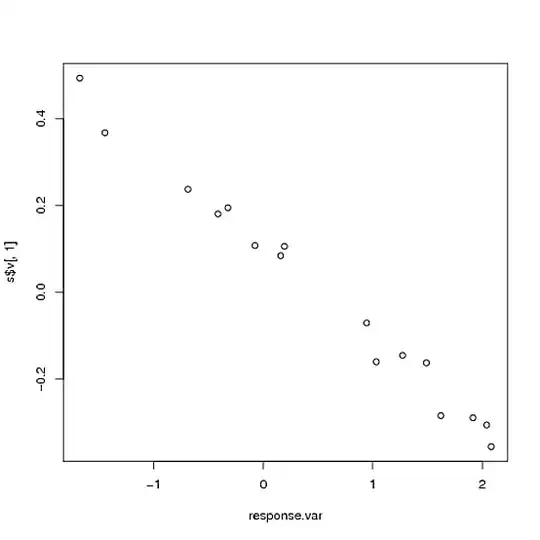
As you can see, the first PC almost perfectly recaptures the response variable that we used to create the matrix (correlation is -.993), even though we put a lot of extra noise in. (Don't worry that the correlation is negative- the direction is arbitrary). Indeed, this correlation with the "eigenmetabolite" is considerably greater than the correlation of the response variable to any of the individual significant genes:

hist(apply(relevant.metabolites, 1, function(r) cor(r, response.var)))

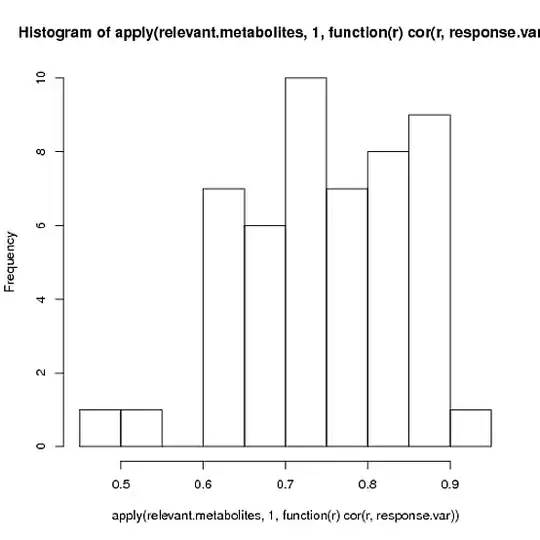
Of course, that's exactly why we're applying PCA in the first place. While the relationship between the response variable and any individual metabolite may be too weak to measure over the rest of the noise, when you combine many genes together you might find that a principal component captures that response well!

Answer 2

After the great discussion, above, I'm hesitant to add another idea, but it seems to me that partial least squares may do what you want, more easily. I usually do this in SAS, so I don't know the details of doing it in R, but there is a PLS package that does both partial least squares regression and principal component regression.

The essential idea behind PLS is that it incorporates both relations among the independent variables and between the independent and dependent variables.