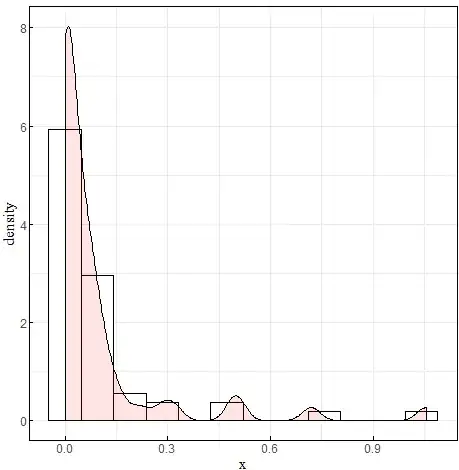
I have a yield loss data(due to some climate disasters) for each year as below, I want to fit the dataset with some distribution function such as normal, weibull, gumbel and so on, It seems like a weibull distribution from the histogram plot, but the goodness of fit result show a bad Q-Q plot, and the k-s test reject as a weibull distribution.
It seems that there are some outliers or unexpected higher values in the tail? should I fit with a discrete probability distribution such as poison?
should I try another distribution function, or my dataset is not suitale for any distribution function, any one can give me some advice?
x=c(0, 0.094, 0.491, 0, 0.029, 0.049, 0.219, 0.068, 0.051, 0.507, 0.086, 0.028, 0, 0.021, 0, 0.162, 0, 0.096, 0.088, 0.061, 0, 0.099, 0.113, 0, 0.319, 0.282, 0.016, 1.055, 0.064, 0.062, 0, 0.719, 0.123, 0, 0, 0.033, 0, 0.062, 0, 0.024, 0, 0, 0.065, 0, 0.143, 0.048, 0, 0, 0, 0.037, 0, 0, 0, 0, 0.025, 0.036, 0)
simple test code in R are as below:
require(fitdistrplus)
fit=fitdist(x+0.0001,"weibull")
plot(fit)
gof=gofstat(fit,fitnames="weibull")
gof$kstest