Goodness of fit for long-tailed distributed data

Question

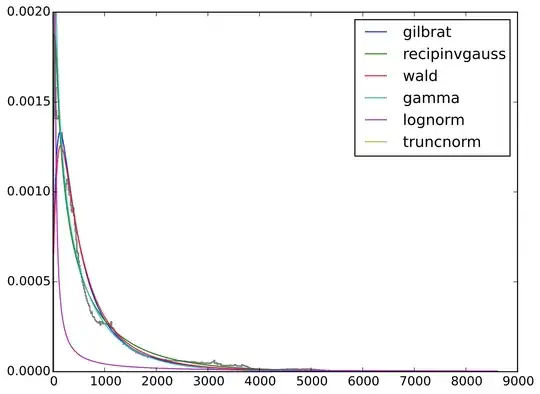
I'm trying to fit a distribution to a set of data (the elevation of all land areas in the world). The histogram shows a long-tailed distribution, and I'd like to see which of the long-tailed models describes it better. I'm running everything on Python.

This is what I am doing so far (data comes from a txt file with about 150k lines, you can get it here):

import sys, os, csv
import math as m
import numpy as np
import scipy as sp
import scipy.stats as ss
import matplotlib.pyplot as plt
import statsmodels.api as sm
from statsmodels.tools import eval_measures as em
import random


# threshold for elevation
cut = 0

# get data
os.chdir(inDir)
fname = 'elevation.txt'
fileIn = open(fname, 'r') 
elev = fileIn.readlines()
elev = [float(x.strip(' \n')) for x in elev]
elev = [x for x in elev if x >= cut]
fileIn.close()
elev = np.array(elev)

# histogram
x = np.arange(min(elev), max(elev), 15) # bin size
size = len(x)
h = plt.hist(elev, bins=size, color='grey', normed=True, histtype='step')

# exogenic var for OLS (x)
exog = h[0]
dist_name = 'gamma' # also testing fo 'gilbrat', 'recipinvgauss', 'wald', 'lognorm', 'truncnorm'
dist = getattr(ss, dist_name)
param = dist.fit(elev)
pdf_fitted = dist.pdf(x, *param[:-2], loc=param[-2], scale=param[-1])

# OLS goodness of fit
# endogenic var (y)
endog = pdf_fitted
model = sm.OLS(endog, exog)
ols_fit = model.fit()
fvalue = ols_fit.fvalue
f_pvalue = ols_fit.f_pvalue
mse_model = ols_fit.mse_model
mse_resid = ols_fit.mse_resid
mse_total = ols_fit.mse_total
params_fit = ols_fit.params
pvalues = ols_fit.pvalues
rsquared = ols_fit.rsquared
resid = ols_fit.resid
rmse = em.rmse(exog,resid)

So my question is: What would be a good value to use as a measure of goodness-of-fit for each of the long-tailed models? Can I use the RMSE here? In a plot of the fitted distributions over the histogram, recipinvgauss looks really good but I'd like something more than just a visual comparison.

Answer 1

The Kolmogorov–Smirnov test offers a way to compare a sample to a theoretical distribution. For more information see:

https://en.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test

Answer 2

Kolmogorov_Smirnov test is an option but it is more sensitive to deviations in the center than in the tails. Anderson Darling test statistic puts more weight in the tails than the KS-test. There are also goodness-of-fit tests in the Von-Mises group with different weighting schemes.

RMSE will be an approximation to the integrated means squared error, IMSE, which is also used in kernel density estimation as a distance measure.

The test statistics of the goodness of fit tests can be used as a distance measure to rank distributions, however as hypothesis tests they have a non-standard distribution that depends in many cases on the parameters and cannot be tabulated. P-values for standard KS or AD tests will not be correct if some parameters are estimated.

Similar to gung's comment: The choice of weights for different parts of the distribution will depend on the intended use.

An alternative is to estimate the tail separately from the main part of the distribution which I have seen in related cases when the emphasis is on modeling the tail. For example, the tails will asymptotically follow a few possible patterns and a common approach is to estimate Pareto tails for values beyond a threshold. (E.g. Matlab has a distribution that fits a kernel density to the center part and a Pareto distribution to the tails.)