Intuitive explanation of unit root

Question

How would you explain intuitively what is a unit root, in the context of the unit root test?

I'm thinking in ways of explaining much like I've founded in this question.

The case with unit root is that I know (little, by the way) that the unit root test is used to test for stationarity in a time series, but it's just it.

How would you go to explain it to the layperson, or to a person who has studied a very basic probability and statistics course?

UPDATE

I accepted whuber's answer as it is what most reflect what I asked here. But I urge everybody that came here to read Patrick's and Michael's answers also, as they are the natural "next step" in understanding the Unit Root. They use mathematics, but in a very intuitive way.

Answer 1

He had just come to the bridge; and not looking where he was going, he tripped over something, and the fir-cone jerked out of his paw into the river.

"Bother," said Pooh, as it floated slowly under the bridge, and he went back to get another fir-cone which had a rhyme to it. But then he thought that he would just look at the river instead, because it was a peaceful sort of day, so he lay down and looked at it, and it slipped slowly away beneath him . . . and suddenly, there was his fir-cone slipping away too.

"That's funny," said Pooh. "I dropped it on the other side," said Pooh, "and it came out on this side! I wonder if it would do it again?"

A.A. Milne, The House at Pooh Corner (Chapter VI. In which Pooh invents a new game and eeyore joins in.)

Here is a picture of the flow along the surface of the water:

The arrows show the direction of flow and are connected by streamlines. A fir cone will tend to follow the streamline in which it falls. But it doesn't always do it the same way each time, even when it's dropped in the same place in the stream: random variations along its path, caused by turbulence in the water, wind, and other whims of nature kick it onto neighboring stream lines.

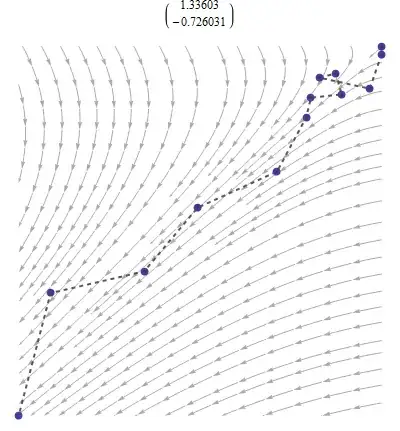
Here, the fir cone was dropped near the upper right corner. It more or less followed the stream lines--which converge and flow away down and to the left--but it took little detours along the way.

---

An "autoregressive process" (AR process) is a sequence of numbers thought to behave like certain flows. The two-dimensional illustration corresponds to a process in which each number is determined by its two preceding values--plus a random "detour." The analogy is made by interpreting each successive pair in the sequence as coordinates of a point in the stream. Instant by instant, the stream's flow changes the fir cone's coordinates in the same mathematical way given by the AR process.

We can recover the original process from the flow-based picture by writing the coordinates of each point occupied by the fir cone and then erasing all but the last number in each set of coordinates.

Nature--and streams in particular--is richer and more varied than the flows corresponding to AR processes. Because each number in the sequence is assumed to depend in the same fixed way on its predecessors--apart from the random detour part--the flows that illustrate AR processes exhibit limited patterns. They can indeed seem to flow like a stream, as seen here. They can also look like the swirling around a drain. The flows can occur in reverse, seeming to gush outwards from a drain. And they can look like mouths of two streams crashing together: two sources of water flow directly at one another and then split away to the sides. But that's about it. You can't have, say, a flowing stream with eddies off to the sides. AR processes are too simple for that.

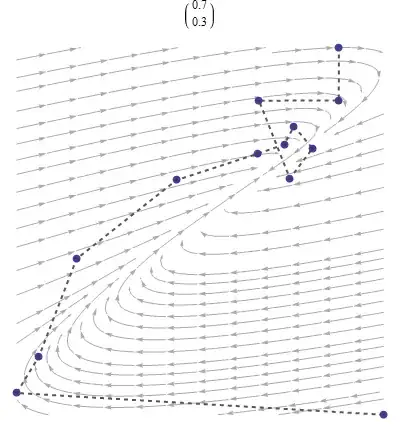
In this flow, the fir cone was dropped at the lower right corner and quickly carried into the eddy in the upper right, despite the slight random changes in position it underwent. But it will never quite stop moving, due to those same random movements which rescue it from oblivion. The fir cone's coordinates move around a bit--indeed, they are seen to oscillate, on the whole, around the coordinates of the center of the eddy. In the first stream flow, the coordinates progressed inevitably along the center of the stream, which quickly captured the cone and carried it away faster than its random detours could slow it down: they trend in time. By contrast, circling around an eddy exemplifies a stationary process in which the fir cone is captured; flowing away down the stream, in which the cone flows out of sight--trending--is non-stationary.

Incidentally, when the flow for an AR process moves away downstream, it also accelerates. It gets faster and faster as the cone moves along it.

The nature of an AR flow is determined by a few special, "characteristic," directions, which are usually evident in the stream diagram: streamlines seem to converge towards or come from these directions. One can always find as many characteristic directions as there are coefficients in the AR process: two in these illustrations. Associated with each characteristic direction is a number, its "root" or "eigenvalue." When the size of the number is less than unity, the flow in that characteristic direction is towards a central location. When the size of the root is greater than unity, the flow accelerates away from a central location. Movement along a characteristic direction with a unit root--one whose size is $1$--is dominated by the random forces affecting the cone. It is a "random walk." The cone can wander away slowly but without accelerating.

(Some of the figures display the values of both roots in their titles.)

Even Pooh--a bear of very little brain--would recognize that the stream will capture his fir cone only when all the flow is toward one eddy or whirlpool; otherwise, on one of those random detours the cone will eventually find itself under the influence of that part of the flow with a root greater than $1$ in magnitude, whence it will wander off downstream and be lost forever. Consequently, an AR process can be stationary if and only if all characteristic values are less than unity in size.

Economists are perhaps the greatest analysts of time series and employers of the AR process technology. Their series of data typically do not accelerate out of sight. They are concerned, therefore, only whether there is a characteristic direction whose value may be as large as $1$ in size: a "unit root." Knowing whether the data are consistent with such a flow can tell the economist much about the potential fate of his pooh stick: that is, about what will happen in the future. That's why it can be important to test for a unit root. A fine Wikipedia article explains some of the implications.

Pooh and his friends found an empirical test of stationarity:

Now one day Pooh and Piglet and Rabbit and Roo were all playing Poohsticks together. They had dropped their sticks in when Rabbit said "Go!" and then they had hurried across to the other side of the bridge, and now they were all leaning over the edge, waiting to see whose stick would come out first. But it was a long time coming, because the river was very lazy that day, and hardly seemed to mind if it didn't ever get there at all.

"I can see mine!" cried Roo. "No, I can't, it's something else. Can you see yours, Piglet? I thought I could see mine, but I couldn't. There it is! No, it isn't. Can you see yours, Pooh?"

"No," said Pooh.

"I expect my stick's stuck," said Roo. "Rabbit, my stick's stuck. Is your stick stuck, Piglet?"

"They always take longer than you think," said Rabbit.

This passage, from 1928, could be construed as the very first "Unit Roo test."

Answer 2

Imagine two $AR(1)$ processes:

• Process 1: $v_k = 0.5 v_{k-1} + \epsilon_{k-1}$
• Process 2: $v_k = v_{k-1} + \epsilon_{k-1}$
• $\epsilon_i$ is drawn from $N(0,1)$

Process 1 has no unit root. Process 2 has a unit root. You can confirm this by calculating characteristic polynomials per Michael's answer.

Imagine we start both processes off at zero, i.e. $v_1 = 0$. Now imagine what happens when we have a "good run" of positive epsilons, and imagine that both process get to $v_{10} = 5$.

What happens next? Where do we expect the sequence to go?

We expect that $\epsilon_{i} = 0$. So we expect that Process 1 case to have $v_{11} = 2.5$, $v_{12} = 1.25$, $v_{13} = 0.625$ etc.

But we expect for Process 2 that $v_{11} = 5$, $v_{12} = 5$, $v_{13} = 5$ etc.

So one intuition is, when a "run of good/bad luck" pushes a process with a unit root around, the sequence "gets stuck in position" by the historical good or bad luck. It will still shift around randomly, but there's nothing "forcing it back". On the other hand, when there's no unit root and the process doesn't blow up, there's a "force" on the process which will make the process drift back to the old position, although the random noise will still knock it around a bit.

The "getting stuck" can include undamped oscillations, a simple example is: $v_k = -v_{k-1} + \epsilon_{k-1}$. This will bounce back and forth positive to negative, but the oscillation is not predestined to explode out to infinity or damp down to zero. You can get more forms of "getting stuck" which include more complex kinds of oscillations.

Answer 3

Consider the first-order autoregressive process $$X_t= aX_{t-1} + e_t$$ where $e_t$ is white noise. The model can also be expressed with all $X$'s on one side as $$X_t-aX_{t-1} = e_t.$$

Using the backshift operator $BX_t = X_{t-1}$ we can re-express the model compactly as $X_t-aBX_t =e_t$ or, equivalently, $$(1-aB)X_t = e_t.$$ The characteristic polynomial is $1-ax$. This has a (unique) root at $x=1/a$. Then for $|a|\lt 1$ we have a stationary $AR(1)$ process and for $|a|\gt 1$ we have an explosive nonstationary $AR(1)$ process. For $a=1$ we have a random walk which is nonstationary and a unit root $x=1/1=1$. So the unit roots form the boundary between stationarity and nonstationarity. The $AR(1)$ model (by virtue of its linear characteristic polynomial) is the simplest to illustrate it.