5

I keep reading everywhere that a time series is non-stationary (e.g. http://en.wikipedia.org/wiki/Unit_root or http://en.wikipedia.org/wiki/Stationary_process) if there's a unit-root. But isn't a larger-than-one root also means the series is non-stationary? Why don't people say that roots larger than unit imply non-stationarity instead?

Intuitive explanation of unit root is a much more general question and indeed the top answer has one sentence in the long essay addresses this question. For those who's only interested in the answer to my question and did not want to read the whole thing (which is epic by the way): "Economists are perhaps the greatest analysts of time series and employers of the AR process technology. Their series of data typically do not accelerate out of sight. They are concerned, therefore, only whether there is a characteristic direction whose value may be as large as 1 in size: a "unit root."

Community
  • 1
RAY
  • 153
  • 5

2 Answers2

8

I think this is actually a quite good question, which is often neglected (as you have noticed) and which I myself haven't thought about much before. The main point, I would say, is that processes with larger-than-one roots (called explosive roots) are not as interesting. If you have something which is just slightly above one, the process will fairly quickly just look like a nice curve. An explosive process will therefore reveal itself, but the (visual) difference between a unit root process and a near-unit root process is much more subtle.

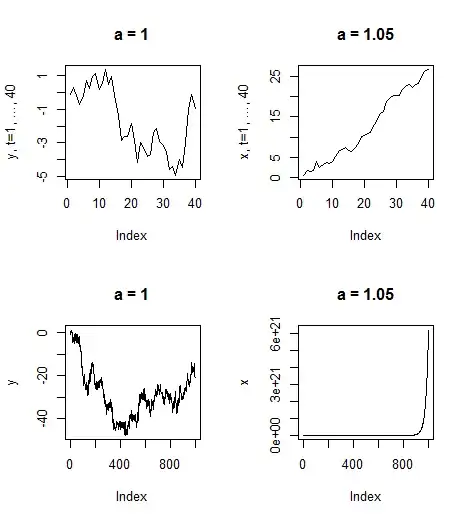
Consider the AR(1) process $$ y_t=ay_{t-1}+\epsilon_t. $$ I have simulated this with $a=1$ (this is the $y_t$ process in the figures), which is a random walk with a unit root. Also shown is $x_t$ which is the same as above but with a slight perturbation, so $a=1.05$ now. Thus, it has an explosive (not just a unit) root. As you can see, the behavior they exhibit is quite different (granted this is just one simulation, of course). You see the trending-like behavior already with $T=40$, and with $T=1000$ it just looks odd. Therefore, as I see it, you disregard the possibility of an explosive root many times because it is "unrealistic". A process such as what you have in the top right panel might instead, in practice, be modeled using deterministic trends with a possible non-stationary process moving around this trend.

So, non-stationarity is definitely implied by explosive roots. But in practice these are much less often found, so we spend quite some time learning about the more realistic situation of non-stationarity, which is a unit root. For the same reason, you often don't learn a whole lot about a negative unit root (i.e. $a=-1$ in the model above).

enter image description here

eps  <- rnorm(1000)
eps2 <- rnorm(1000)
y <- eps
x <- eps2
for (t in 2:1000) {
  y[t] <- y[t-1] + eps[t]
  x[t] <- 1.05*x[t-1] + eps2[t]
}

par(mfrow=c(2,2))
plot(y[1:40], type = "l", ylab = "y, t=1, ..., 40", main = "a = 1")
plot(x[1:40], type = "l", ylab = "x, t=1, ..., 40", main = "a = 1.05")
plot(y, type = "l", main = "a = 1")
plot(x, type = "l", main = "a = 1.05")
hejseb
  • 2,298
  • 1
  • 15
  • 26
1

There are several kinds of non-stationarities:

1) Series expected value is a function of time
2) Series variance depends on time and not just about lag
3) Etc

Series with linear trend is non-stationary but stationary around trend..

EDIT:

Your example of stochastic difference equation with explosive root is of course non-stationary if you take definition from non time independent variance or expected value.

But linear trend is more interesting as a mathematical model than explosive stochastic difference equation.

Analyst
  • 2,527
  • 10
  • 11
  • 1
    How exactly does this answer any of the two questions "But isn't a larger-than-one root also means the series is non-stationary?" or "Why don't people say that roots larger than unit imply non-stationarity instead?"? – hejseb Mar 25 '15 at 06:41
  • @hejseb Added more on edit... – Analyst Mar 25 '15 at 07:11