I am currently running a three-level meta-analysis, due to the fact that I have multiple dependent effect sizes in many studies. I do not know the actual dependencies between effect sizes, however, so when there are dependencies, they are assumed to be $\tau^2_{(3)}$, per Cheung (2015, Ch. 6) and Konstantopoulos (2011). I am using the rma.mv() function in the metafor package to do this and employing a meta-regression approach, such that my effect sizes es (in my meta-analysis, Fisher's Z) are predicted by two moderators, pubyear and subtle. The model looks like this:
mod2.1 <- rma.mv(es ~ pubyear + subtle,
random = ~1|studyid/effectid,
V = var, data = meta)
My main interest is in pubyear. I find that, after adding subtle as an additional covariate, the effect of pubyear gets smaller.
This leads me to ask the question: Is subtle predicted by pubyear? I do not know how I would estimate this, so my question is: How can I model the relationship between two moderators in a meta-regression?
Right now, my meta-analysis shows that the es gets smaller as pubyear increases, so now I want to know: Has the subtlety of measures (subtle) also increased over time (pubyear)? How would I do this?
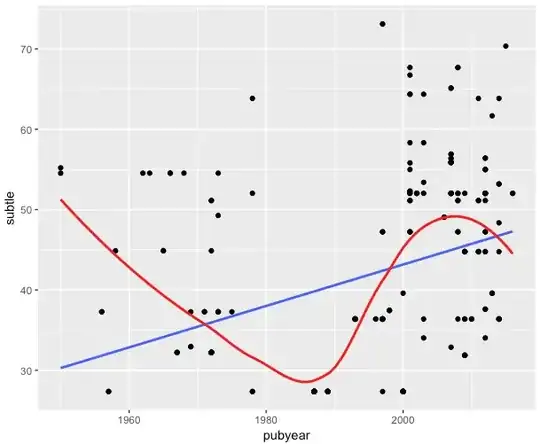
The intuitive solution would to simply correlate the two with one another. But this does not take into account that one study might report 8 effect sizes, while another study may only report 1. Obviously, the study with 8 effect sizes will have more weight. I plotted this relationship, regardless. You can see that there may be a relationship when doing this weirdly-weighted regression (lm line in blue, loess line in red):
Has anyone run into this before or know how to handle it?