nls() gradient error in fitting growth curve data

Question

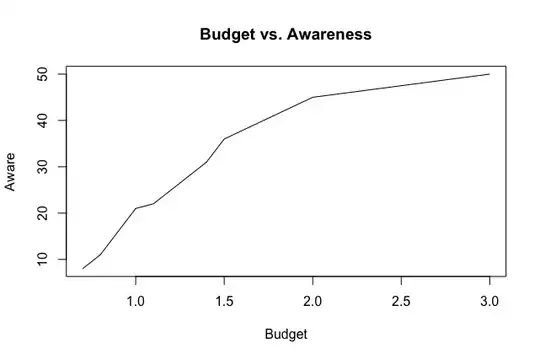
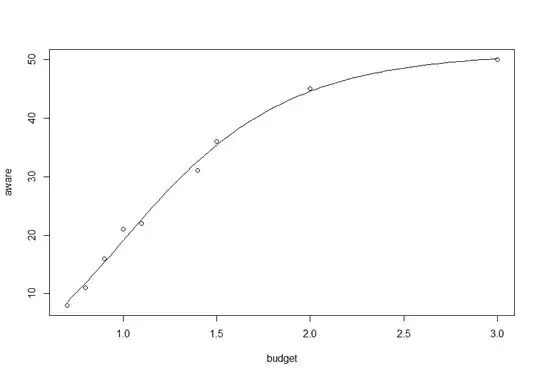
I am trying to model the following data on promotional budget and customer awareness. The idea is, at some point, increase in budget doesn't have any further impact on awareness; it saturates.

> promo
  budget aware
1    0.7     8
2    0.8    11
3    0.9    16
4    1.0    21
5    1.1    22
6    1.4    31
7    1.5    36
8    2.0    45
9    3.0    50

Beyond promo$budget=3.0, there won't be any returns. A plot of the budget and aware shows a growth curve that looks a bit like Gompertz curve.

So, I tried something like this:

f <- nls(aware ~ A*exp(-1*b*exp(-1*c*budget)), data=promo, start=list(A=4,b=1,c=-2))

It results in this error:

Error in nls(aware ~ A * exp(-1 * b * exp(-1 * c * budget)), data = promo,  : singular gradient

How do I fit the growth curve to this data?

Answer 1

Use a self-starting model:

promo <- read.table(text = "  budget aware
1    0.7     8
2    0.8    11
3    0.9    16
4    1.0    21
5    1.1    22
6    1.4    31
7    1.5    36
8    2.0    45
9    3.0    50")

f <- nls(aware ~ SSgompertz(budget, Asym, b2, b3), data=promo)

plot(aware ~ budget, data = promo)
curve(predict(f, newdata = data.frame(budget = x)), add = TRUE)

Note that SSgompertz uses a different parameterization, see help("SSgompertz"). However, your problem are the starting values. For instance, you start with an asymptote value of 4, which obviously is far from the actual value. If I set start = list(A = 50, b = 0.1, c = 1) I get a successful (and identical) fit with your parameterization.