0

I have read this article and those linked to it, but I am still having difficulties fitting a function of this form to data I have using the nls function in R. Invariably, I fail to get convergence regardless of what starting values I choose for A through C.

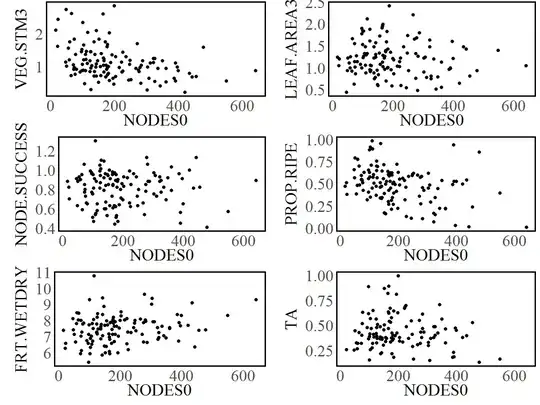
Here is a plot of all six of the relationships I would ultimately like to fit: enter image description here

While VEG.STM3 and PROP.RIPE probably will conform to a curve of this shape fairly well, the others probably won't, and that's fine. I still have a justifiable reason for trying it.

My questions are as follows:

  1. What are the parameters A, B, and C doing, mathematically, in a function of this form? A appears to be the Y asymptote, B seems to be a scalar of some kind, and C seems to control the rate of decay, but, beyond that, I can't seem to figure out what a reasonable range of values for each parameter should be, especially from one set of data to the next.
  2. Is there a way to "linearize" this problem so that lm can be used in place of nls? My understanding is that this function is equivalent to ln(Y) ~ ln(A) + ln(B) + CX, but I don't understand how to fit that equation any more than I understand how to fit this current curve.
  3. Is there any way to get nls to be less fussy and more robust to lousy starting guesses?
  4. Once I get nls to run successfully, how can I compare the fit of the model to one fit by simple linear regression? Would use of AICc be appropriate in that case?

Here is some data to work with:

PROP.RIPE = c(0.37, 0.223, 0.223, 0.224, 0.388, 0.413, 0.406, 0.422, 0.554, 
0.453, 0.569, 0.511, 0.13, 0.166, 0.16, 0.216, 0.297, 0.344, 
0.339, 0.292, 0.601, 0.535, 0.65, 0.535, 0.269, 0.238, 0.334, 
0.272, 0.523, 0.358, 0.449, 0.393, 0.458, 0.426, 0.576, 0.468, 
0.581, 0.579, 0.527, 0.568, 0.348, 0.313, 0.317, 0.267, 0.623, 
0.527, 0.646, 0.589, 0.488, 0.444, 0.498, 0.449, 0.109, 0.103, 
0.171, 0.153, 0.505, 0.343, 0.345, 0.213, 0.029, 0.011, 0.071, 
0.013, 0.697, 0.604, 0.624, 0.639, 0.386, 0.508, 0.38, 0.471, 
0.618, 0.488, 0.513, 0.485, 0.602, 0.597, 0.625, 0.495, 0.318, 
0.457, 0.423, 0.547, 0.88, 0.949, 0.912, 0.771, 0.628, 0.635, 
0.486, 0.567, 0.621, 0.549, 0.698, 0.709, 0.541, 0.563, 0.789, 
0.692, 0.525, 0.395, 0.449, 0.597, 0.57, 0.487, 0.556, 0.546, 
0.495, 0.617, 0.754, 0.71, 0.585, 0.719, 0.508, 0.536, 0.592, 
0.472, 0.481, 0.658, 0.937, 0.853, 0.981, 0.887)

NODES0 = c(124L, 362L, 198L, 343L, 152L, 193L, 98L, 167L, 148L, 284L, 
113L, 137L, 227L, 323L, 156L, 362L, 166L, 327L, 137L, 312L, 166L, 
350L, 97L, 222L, 182L, 456L, 143L, 277L, 172L, 272L, 110L, 184L, 
138L, 288L, 102L, 124L, 236L, 280L, 159L, 127L, 104L, 176L, 93L, 
167L, 178L, 400L, 126L, 248L, 189L, 336L, 181L, 304L, 245L, 283L, 
151L, 327L, 116L, 179L, 144L, 177L, 397L, 642L, 322L, 443L, 125L, 
249L, 100L, 144L, 56L, 22L, 23L, 17L, 252L, 387L, 184L, 308L, 
115L, 267L, 82L, 157L, 223L, 226L, 79L, 73L, 101L, 139L, 104L, 
60L, 200L, 164L, 66L, 49L, 173L, 204L, 64L, 107L, 435L, 215L, 
51L, 129L, 392L, 550L, 174L, 178L, 276L, 204L, 98L, 74L, 421L, 
303L, 126L, 150L, 168L, 195L, 77L, 75L, 72L, 142L, 59L, 47L, 
391L, 479L, 109L, 111L)

NODE.SUCCESS = c(1.05, 0.79, 0.86, 0.69, 0.85, 0.8, 0.77, 0.84, 0.53, 0.88, 
0.88, 0.79, 0.85, 0.88, 1, 1.03, 0.95, 0.77, 0.92, 0.73, 0.98, 
0.92, 0.97, 0.99, 0.88, 0.82, 0.84, 0.78, 0.63, 0.54, 0.54, 0.47, 
1.09, 0.88, 0.95, 0.99, 0.96, 1.13, 0.91, 1.01, 0.81, 0.89, 0.99, 
0.85, 0.95, 0.65, 0.87, 0.73, 0.64, 0.82, 0.82, 0.75, 0.93, 1.06, 
0.94, 0.89, 0.65, 0.53, 0.6, 0.62, 0.91, 0.89, 0.93, 1.13, 0.81, 
0.63, 0.75, 0.67, 0.93, 0.82, 0.7, 0.88, 0.8, 0.96, 0.9, 0.94, 
0.58, 0.66, 0.65, 0.63, 0.66, 0.62, 0.66, 0.77, 0.51, 0.6, 0.47, 
0.9, 0.69, 0.73, 0.59, 0.63, 0.97, 0.93, 0.95, 0.91, 0.81, 0.92, 
0.88, 1.1, 0.56, 0.57, 0.44, 0.51, 0.85, 0.83, 0.96, 0.85, 1, 
0.97, 0.94, 0.95, 0.61, 0.71, 0.73, 0.8, 1.06, 0.96, 0.9, 0.91, 
0.45, 0.41, 1.3, 0.55)
Community
  • 1
Bajcz
  • 515
  • 1
  • 4
  • 19

0 Answers0