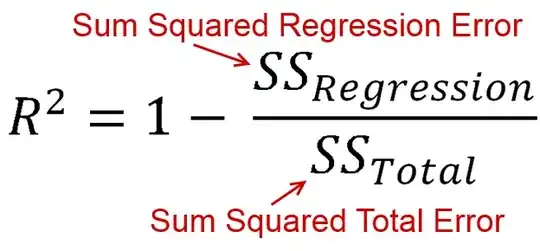Let's say I have some data, and then I fit the data with a model (a non-linear regression). Then I calculate the R-squared ($R^2$).
When R-squared is negative, what does that mean? Does that mean my model is bad? I know the range of $R^2$ can be [-1,1]. When $R^2$ is 0, what does that mean as well?
$R^2$ can be negative, it just means that:
To the people saying that $R^2$ is between 0 and 1, this is not the case. While a negative value for something with the word 'squared' in it might sound like it breaks the rules of maths, it can happen in an $R^2$ model without an intercept. To understand why, we need to look at how $R^2$ is calculated.
This is a bit long - If you want the answer without understanding it, then skip to the end. Otherwise, I've tried to write this in simple words.
First, let's define 3 variables: $RSS$, $TSS$ and $ESS$.
Calculating RSS:
For every independent variable $x$, we have the dependent variable $y$. We plot a linear line of best fit, which predicts the value of $y$ for each value of $x$. Let's call the values of $y$ the line predicts $\hat y$. The error between what your line predicts and what the actual $y$ value is can be calculated be subtraction. All these differences are squared and added up, which gives the Residual Sum of Squares $RSS$.
Putting that into an equation, $RSS = \sum (y - \hat y)^2$
Calculating TSS:
We can calculate the average value of $y$, which is called $\bar y$. If we plot $\bar y$, it is just a horizontal line through the data because it is constant. What we can do with it though, is subtract $\bar y$ (the average value of $y$) from every actual value of $y$. The result is squared and added together, which gives the total sum of squares $TSS$.
Putting that into an equation $TSS = \sum (y - \bar y)^2$
Calculating ESS:
The differences between $\hat y$ (the values of $y$ predicted by the line) and the average value $\bar y$ are squared and added. This is the Explained sum of squares, which equals $\sum (\hat y - \bar y)^2$
Remember, $TSS = \sum (y - \bar y)^2$, but we can add a $ + \hat y - \hat y$ into it, because it cancels itself out. Therefore, $TSS = \sum (y - \hat y + \hat y -\bar y)^2$. Expanding these brackets, we get $TSS = \sum (y - \hat y)^2 + 2* \sum (y - \hat y)(\hat y - \bar y) + \sum (\hat y - \bar y)^2$
When, and only when the line is plotted with an intercept, the following is always true: $2* \sum (y - \hat y)(\hat y - \bar y) = 0$. Therefore, $TSS = \sum (y - \hat y)^2 + \sum (\hat y - \bar y)^2$, which you may notice just means that $TSS = RSS + ESS$. If we divide all terms by $TSS$ and rearrange, we get $1 - \frac {RSS}{TSS} = \frac {ESS}{TSS}$.
Here's the important part:
$R^2$ is defined as how much of the variance is explained by your model (how good your model is). In equation form, that's $R^2 = 1 - \frac {RSS}{TSS}$. Look familiar? When the line is plotted with an intercept, we can substitute this as $R^2 = \frac {ESS}{TSS}$. Since both the numerator and demoninator are sums of squares, $R^2$ must be positive.
BUT
When we don't specify an intercept, $2* \sum (y - \hat y)(\hat y - \bar y)$ does not necessarily equal $0$. This means that $TSS = RSS + ESS + 2* \sum (y - \hat y)(\hat y - \bar y)$.
Dividing all terms by $TSS$, we get $1 - \frac{RSS}{TSS} = \frac {ESS + 2* \sum (y - \hat y)(\hat y - \bar y)}{TSS}$.
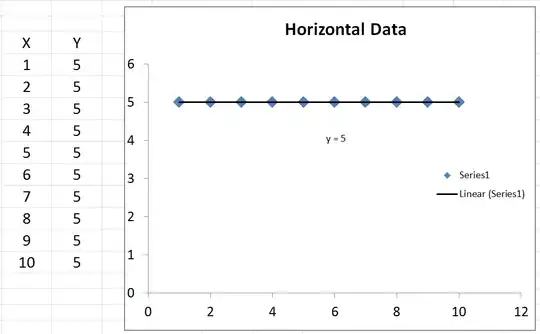
Finally, we substitute to get $R^2 = \frac {ESS + 2* \sum (y - \hat y)(\hat y - \bar y)}{TSS}$. This time, the numerator has a term in it which is not a sum of squares, so it can be negative. This would make $R^2$ negative. When would this happen? $2* \sum (y - \hat y)(\hat y - \bar y)$ would be negative when $y - \hat y$ is negative and $\hat y - \bar y$ is positive, or vice versa. This occurs when the horizontal line of $\bar y$ actually explains the data better than the line of best fit.
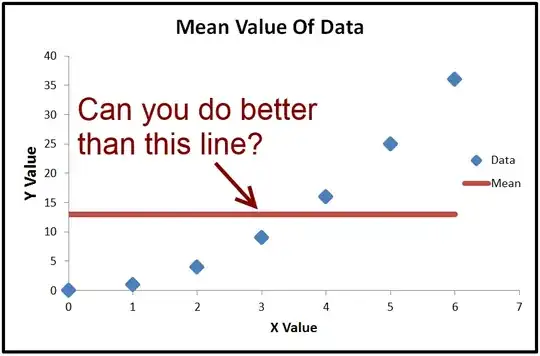
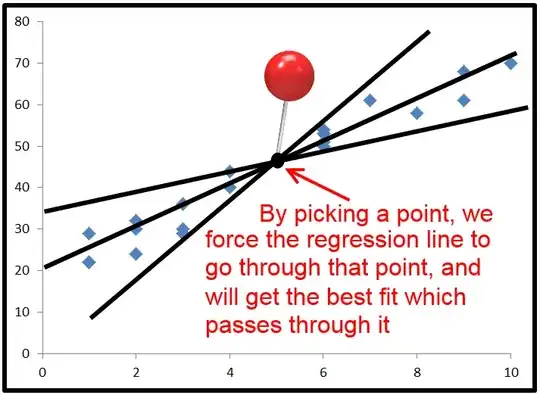
Here's an exaggerated example of when $R^2$ is negative (Source: University of Houston Clear Lake)
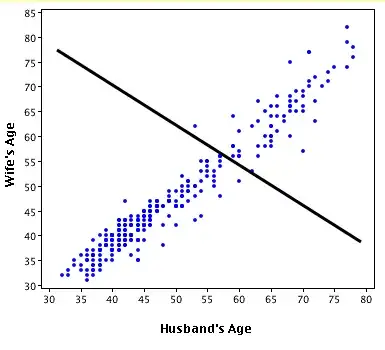
Put simply:
You also asked about $R^2 = 0$.
I commend you for making it through that. If you found this helpful, you should also upvote fcop's answer here which I had to refer to, because it's been a while.
Neither answer so far is entirely correct, so I will try to give my understanding of R-Squared. I have given a more detailed explanation of this on my blog post here "What is R-Squared"
Sum Squared Error
The objective of ordinary least squared regression is to get a line which minimized the sum squared error. The default line with minimum sum squared error is a horizontal line through the mean. Basically, if you can't do better, you can just predict the mean value and that will give you the minimum sum squared error
R-Squared is a way of measuring how much better than the mean line you have done based on summed squared error. The equation for R-Squared is
Now SS Regression and SS Total are both sums of squared terms. Both of those are always positive. This means we are taking 1, and subtracting a positive value. So the maximum R-Squared value is positive 1, but the minimum is negative infinity. Yes, that is correct, the range of R-squared is between -infinity and 1, not -1 and 1 and not 0 and 1
What Is Sum Squared Error
Sum squared error is taking the error at every point, squaring it, and adding all the squares. For total error, it uses the horizontal line through the mean, because that gives the lowest sum squared error if you don't have any other information, i.e. can't do a regression.
As an equation it is this
Now with regression, our objective is to do better than the mean. For instance this regression line will give a lower sum squared error than using the horizontal line.
The equation for regression sum squared error is this
Ideally, you would have zero regression error, i.e. your regression line would perfectly match the data. In that case you would get an R-Squared value of 1
Negative R Squared
All the information above is pretty standard. Now what about negative R-Squared ?
Well it turns out that there is not reason that your regression equation must give lower sum squared error than the mean value. It is generally thought that if you can't make a better prediction than the mean value, you would just use the mean value, but there is nothing forcing that to be the cause. You could for instance predict the median for everything.
In actual practice, with ordinary least squared regression, the most common time to get a negative R-Squared value is when you force a point that the regression line must go through. This is typically done by setting the intercept, but you can force the regression line through any point.
When you do that the regression line goes through that point, and attempts to get the minimum sum squared error while still going through that point.
By default, the regression equations use average x and average y as the point that the regression line goes through. But if you force it through a point that is far away from where the regression line would normally be you can get sum squared error that is higher than using the horizontal line
In the image below, both regression lines were forced to have a y intercept of 0. This caused a negative R-squared for the data that is far offset from the origin.
For the top set of points, the red ones, the regression line is the best possible regression line that also passes through the origin. It just happens that that regression line is worse than using a horizontal line, and hence gives a negative R-Squared.
Undefined R-Squared
There is one special case no one mentioned, where you can get an undefined R-Squared. That is if your data is completely horizontal, then your total sum squared error is zero. As a result you would have a zero divided by zero in the R-squared equation, which is undefined.
As the previous commenter notes, r^2 is between [0,1], not [-1,+1], so it is impossible to be negative. You cannot square a value and get a negative number. Perhaps you are looking at r, the correlation? It can be between [-1,+1], where zero means there is no relationship between the variables, -1 means there is a perfect negative relationship (as one variable increases, the other decreases), and +1 is a perfect positive relationship (both variables go up or down concordantly).
If indeed you are looking at r^2, then, as the previous commenter describes, you are probably seeing the adjusted r^2, not the actual r^2. Consider what the statistic means: I teach behavioral science statistics, and the easiest way that I've learned to teach my students about the meaning of r^2 is " % variance explained." So if you have r^2=0.5, the model explains 50% of the variation of the dependent (outcome) variable. If you have a negative r^2, it would mean that the model explains a negative % of the outcome variable, which is not an intuitively reasonable suggestion. However, adjusted r^2 takes the sample size (n) and number of predictors (p) into consideration. A formula for calculating it is here. If you have a very low r^2, then it is reasonably easy to get negative values. Granted, a negative adjusted r^2 does not have any more intuitive meaning than regular r^2, but as the previous commenter says, it just means your model is very poor, if not just plain useless.
The question is asking about "a model (a non-linear regression)". In this case there is no bound of how negative R-squared can be.
R-squared = 1 - SSE / TSS
As long as your SSE term is significantly large, you will get an a negative R-squared. It can be caused by overall bad fit or one extreme bad prediction.
For example:
In [78]: from sklearn import metrics
In [79]: actual = np.array([1,2,3,4,5,6])
In [80]: preds = np.array([1,2,3,4,5,60]) # the model can predict anything
In [81]: metrics.r2_score(actual, preds)
Out[81]: -165.62857142857143
In [82]: sse = np.sum((actual - preds) ** 2)
In [83]: sse
Out[83]: 2916
In [84]: tss = np.sum((actual - np.mean(actual)) ** 2)
In [85]: tss
Out[85]: 17.5
In [86]: r_2 = 1 - sse / tss
In [87]: r_2
Out[87]: -165.62857142857143
