How can $R^2$ have two different values for the same regression (without an intercept)

Question

My question is multifaceted. So I'll start by asking my question and then explain what has caused me to ask this question.

How can I calculate the coefficient of determination for a linear regression with a defined y-intercept? The y-variable is the dependent variable and the x-variable is the independent variable. For example, the y-intercept would be set equal to 0 when the x-variable is 0. The equation of the line would be y = mx + b and b = 0.

My question came about when I was trying to plot experimentally measured fluid flow data. I am plotting my data in a way that compares the data to Darcy's Law, a phenomenological model for fluid flow through porous media that says for certain conditions the volumetric flow rate is proportional to pressure gradient.

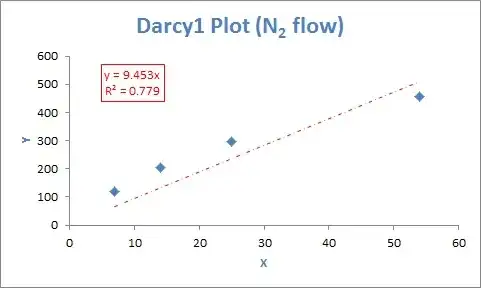
Below is my dataset and my plot of the data.

x: {54, 25, 14, 7}

y: {458, 295, 204, 118}

Note*: For simplicity here, I rounded my dataset numbers to the nearest whole number.

I plotted the data in Microsoft Excel and applied a linear trendline with a the y-intercept set to zero. I applied the trendline this way because based on Darcy's Law the y-variable (volumetric flow rate) should be zero when the x-variable (pressure gradient) is equal to zero. Displaying the coefficient of determination on the plot, Excel shows it to be, R2 = 0.779.

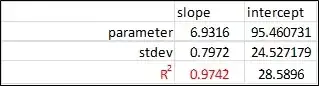
When I use Microsoft Excel's LINEST function I get a coefficient of determination, R2 = 0.9602, as seen in the image below.

For the LINEST function I used: =LINEST(known y's, known x's, FALSE, TRUE), where in the third argument I used "FALSE" to set the y-intercept, b, equal to zero.

There is a discrepancy between the two coefficients of determination given by Excel, 0.779 versus 0.9602.

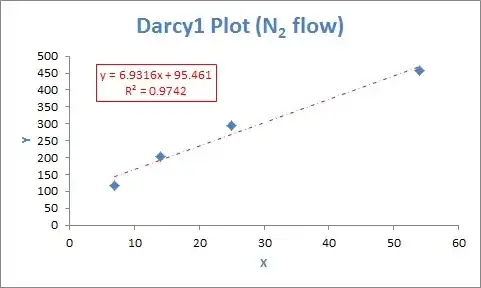
Furthermore, if I tell Excel's LINEST function to calculate the regression without a set intercept, e.g. := LINEST(known y's, known x's, TRUE, TRUE), where the third argument I used "TRUE" to, as Excel claims, "to calculate b normally". I get a coefficient of determination, R2 = 0.9742, as seen in the image below.

This R2 value matches the graphical output Excel provides for the R2 value if I format the plot's trendline to not have a set y-intercept, as seen in the image below.

Since Excel calculated the same R2 value for a trendline without a set y-intercept, this leads me to believe there is something erroneous with the LINEST function when tryint to set y-intercept to zero (using "FALSE" as the third argument).

I have read multiple times that one should really not use Excel for any but the simplest of statistics, and sometimes not even then because Excel has a bunch of "gotchyas".

If I want to calculate the coefficient of determination by hand, how can I do it? Further, what is going on with Excel, why is it calculating different values? I am using Excel 2010.

Answer 1

I think this is an interesting question (+1), not because of Excel but because of the fact that it points out that there are two different definitions of $R^2$ and apparently Excel mixes both!

As I said in my comment, because of the 'problem' described in Can the coefficient of determination $R^2$ be more than one? What is its upper bound?, there are two definitions of $R^2$:

Let us first introduce some notation: your data are denoted as $y$ for the dependent variable and $x$ for the indpendent variable. You estimate a coefficient with the trend on the graph and with the linest function, you find $9.4382$. So you find that you can ''approximate'' $y$ by $\hat{y}= 9.4382 \times x$. So with your values for $x$ you find $\hat{y} = (509.66, 235.95, 132.13, 66.07)$. Obviously, $\hat{y}$ will not be identical to $y$ and you have a residual $\hat{u}= y - \hat{y} = (-51.66, 59.04, 71.86, 51.93)$.

Further we will need the average of $y$, let's call it $\bar{y}=268.75$.

$R^2$ for a model with an intercept:

The 'usual' defintion of $R^2$ is computed as follows:

1. take, the residuals $\hat{u}$, square them, and add them up, tis is the residual sum of squares, in your case you find $RSS=$14016.96;
2. From each value of $y$, subtract the average, square all these numbers and add them up, this is the total sum of squares, in your case you have $TSS=63422.75$;
3. $R^2$ is now equal to $1-\frac{RSS}{TSS}=1-\frac{14016.96}{63422.75}=0.7789$, this is approximately the value you find in your graph (the difference is probably due to rounding errors).

$R^2$ for a model without an intercept:

Because of the problems with $R^2$ in a model without an intercept (see Can the coefficient of determination $R^2$ be more than one? What is its upper bound?), there is another defintion of $R^2$ for such a model:

1. Take your $y$ values, square them, and add up these squares, you find $352329 $;
2. Do the same for $\hat{y}$, you find, $337255.4384$;
3. The $R^2$ is the second divided by the first, you find $0.957$, which is up to rouding errors your other value for $R^2$ that you have mentioned.

As you see, excell has the first value in the graph for the trendline, and with 'linest' it has the second value. As the second value is the one for a model without an intercept, I would say that 'linest' is closer, but in general I would say that you should avoid models without an intercept.

EDIT: because of your question in the comments I added this:

@jake mcgregor

You asked "could you explain your last statement a bit?", I assume that this means ''why should I avoid models without an intercept?''

The regression model $y=\beta_0 + \beta_1 x + \epsilon$ makes several assumptions, and when these assumptions are fullfilled then the estimated values of the $\beta_i$ have ''nice'' properties like unbiasedness ('right' on average), consistency (better and better as sample size increase) and efficiency (smallest variance).

One of the assumptions is that the error term $\epsilon$ is has a mean that is equal to zero. If that assumption is not fullfilled then these 'nice' properties can not be shown.

The assumption that $\epsilon$ has mean zero is not very restrictive, at least if your model has an intercept: indeed if the mean of error would not be zero , than, by adding the mean to the intercept $\beta_0$ it will be zero !

If you do not have an intercept, then this does not work, so if you do not include the intercept in your model, you have to be certain that the errors $\epsilon$ are zero on average, in other words you will have to have some theoretical result that 'guarantees' you that your line will pass through the origin (note these are two restrictions: 'line' and 'through the origin'), so you have to be sure about the functional form and the 'through the origin'.

If you have no theoretical or other justfication for 'function through the origin' then it's just an assumption, but if your assumption is violated then the estimates of the coefficients may be biased.

Answer 2

I can't answer about the Excel part because I don't know the LINEST function. However, the way Excel calculates the linear trend line is by using Least Squares. Say you want to fit your data to a hypothesis function f(x), which uses a set of parameters $a_1, a_2,...a_N$, then the way to obtain the values $a_1, a_2,...a_N$ is to minimize the error function: $F^{err} = \sum_{i=1}^{n_{samples}} (f(x_i)-y_i)^2 $

Specifically in your case, your hypothesis is $f_1(x) = ax$ and you want to find the appropriate $a_1$. To do so, you need to find $a_1$ such that

$F_1^{err} = \sum_{i=1}^{n_{samples}} (ax_i-y_i)^2 $

is minimal. To do so by hand, you need to take this function, take its derivative with respect to $a_1$ and find the minimum point. This will give you around 9.4.

On a further note, I tried to fit your data into a quadratic form and fits perfectly, so you might want to consider using it. See the figure below