Why does the variance of the Random walk increase?

Question

The random walk that is defined as $Y_{t} = Y_{t-1} + e_t$, where $e_t$ is white noise. Denotes that the current position is the sum of the previous position + an unpredicted term.

You can prove that the mean function $\mu_t = 0 $, since

$$E(Y_{t}) = E(e_1+ e_2+ ... +e_t) = E(e_1) + E(e_2) +... +E(e_t) = 0 + 0 + \cdots + 0$$

But why is it that the variance increases linearly with time?

Does this have something to do with it's not “pure” random, since the new position is very correlated with the previous one?

EDIT:

Now I have a much better understanding by visualizing a big sample of random walks, and here we can easily observe that the overall variance does increase over time,

and the mean is as expected around zero.

Maybe this was trivial after all, since in the very early stages of the time series (compare time = 10 with time = 100) the random walkers have not had yet the time to explore as much.

Answer 1

In short because it keeps adding the variance of the next increments to the variability we have in getting to where we are now.

$\text{Var}(Y_{t}) = \text{Var}(e_1+ e_2+ ... +e_t)$
$\qquad\quad\;\;= \text{Var}(e_1) + \text{Var}(e_2) +... +\text{Var}(e_t)$ (independence)
$\qquad\quad\;\;= \sigma^2 + \sigma^2 + ... + \sigma^2=t\sigma^2\,,$

and we can see that $t\sigma^2$ increases linearly with $t$.

---

The mean is zero at each time point; if you simulated the series many times and averaged across series for a given time, that would average to something near 0

$\quad^{\text{Figure: 500 simulated random walks with sample mean in white and }}$
$\quad^{ \pm \text{ one standard deviation in red. Standard deviation increases with } \sqrt{t}\,.}$

Answer 2

Here's a way to imagine it. To simplify things, let's replace your white noise $e_i$ with a coin flip $e_i$

$$ e_i = \left\{ \begin{array}{c} 1 \ \text{with} \ Pr = .5 \\ -1 \ \text{with} \ Pr = .5 \end{array} \right. $$

this just simplifies the visualization, there's nothing really fundamental about the switch except easing the strain on our imagination.

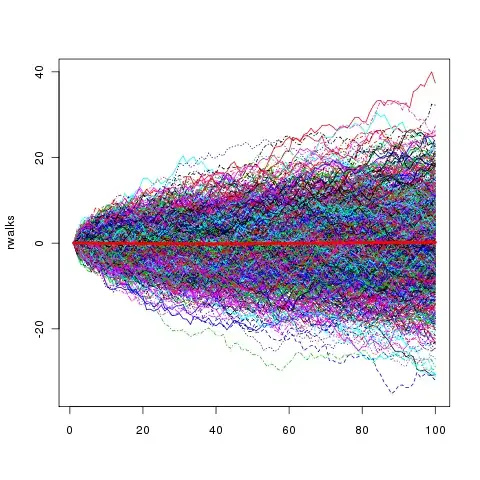
Now, suppose you have gathered an army of coin flippers. Their instructions are to, at your command, flip their coin, and keep a working tally of what their results were, along with a summation of all their previous results. Each individual flipper is an instance of the random walk

$$ W = e_1 + e_2 + \cdots $$

and aggregating over all of your army should give you a take on the expected behavior.

flip 1: About half of your army flips heads, and half flips tails. The expectation of the sum, taken across your whole army, is zero. The maximum value of $W$ across your whole army is $1$ and the minimum is $-1$, so the total range is $2$.

flip 2: About half flip heads, and half flips tails. The expectation of this flip is again zero, so the expectation of $W$ over all flips does not change. Some of your army has flipped $HH$, and some others have flipped $TT$, so the maximum of $W$ is $2$ and the minimum is $-2$; the total range is $4$.

...

flip n: About half flip heads, and half flips tails. The expectation of this flip is again zero, so the expectation of $W$ over all flips does not change, it is still zero. If your army is very large, some very lucky soldiers flipped $HH \cdots H$ and others $TT \cdots T$. That is, there is a few with $n$ heads, and a few with $n$ tails (though this is getting rarer and rarer as time goes on). So, at least in our imaginations, the total range is $2n$.

So here's what you can see from this thought experiment:

• The expectation of the walk is zero, as each step in the walk is balanced.
• The total range of the walk grows linearly with the length of the walk.

To recover intuition we had to discard the standard deviation and use in intuitive measure, the range.

Answer 3

Does this have something to do with it's not "pure" random, since the new position is very correlated with the previous one?

It appears that by "pure" you mean independent. In random walk only the steps are random and independent of each other. As you noted, the "positions" are random but correlated, i.e. not independent.

The expectation of the position is still zero like you wrote $E[Y_t]=0$. The reason why you observe non-zero positions is because the positions are still random, i.e. $Y_t$ are all non zero random numbers. As a matter of fact, while you increase the sample larger $Y_t$ will be observed from time to time, precisely because, as you noted, the variance is increasing with sample size.

The variance is increasing because if you unwrap the position as follows: $Y_t=Y_0+\sum_{i=0}^t\varepsilon_t$, you can see that the position is a sum of steps, obviously. The variances add up with sample size increasing.

By the way, the means of errors also add up, but in a random walk we usually assume that the means are zero, so adding all zeros will still result in zero. There's random walk with a drift: $Y_t-Y_{t-1}=\mu+\varepsilon_t$, where $Y_t$ will drift away from zero at rate $\mu t$ with sample time.

Answer 4

Let's take a different example for an intuitive explanation: throwing darts at a dartboard. We have a player, who tries to aim for the bullseye, which we take to be a coordinate called 0. The player throws a few times, and indeed, the mean of his throws is 0, but he's not really good, so the variance is 20 cm.

We ask the player to throw a single new dart. Do you expect it to hit bullseye?

No. Although the mean is exactly bullseye, when we sample a throw, it's quite likely not to be bullseye.

In the same way, with random walk, we don't expect a single sample at time $t$ to be anywhere near 0. That's in fact what the variance indicates: how far away do we expect a sample to be?

However, if we take a lot of samples, we'll see that it does center around 0. Just like our darts player will almost never hit bullseye (large variance), but if he throws a lot of darts, he will have them centered around the bullseye (mean).

If we extend this example to the random walk, we can see that the variance increases with time, even though the mean stays at 0. In the random walk case, it seems strange that the mean stays at 0, even though you will intuitively know that it almost never ends up at the origin exactly. However, the same goes for our darter: we can see that any single dart will almost never hit bullseye with an increasing variance, and yet the darts will form a nice cloud around the bullseye - the mean stays the same: 0.

Answer 5

Here's another way to get intuition that variance increases linearly with time.

Returns increase linearly with time. $.1\%$ return per month translate into $1.2\%$ return per year - $X$ return per day generate $365X$ return per year (assuming independence).

It makes sense that the range of returns also increases linearly. If monthly return is $.1\%$ on average $\pm .05\%$, then it makes intuitive sense that per year it is $1.2\%$ on average $\pm .6\%$.

Well, if we intuitively think of variance as range, then it makes intuitive sense that variance increases in the same fashion as return through time, that is linearly.

Answer 6

The answer from Glen B already sufficiently and easily/briefly shows why the variance scales linearly with time.

This answer will give an alternative viewpoint. Possibly one might find the equation for the addition of variance not so intuitive or different; and this answer might give an additional intuition from a different angle.

This alternative viewpoint will consider the probability distribution as a solution to a differential equation that relates to a diffusion process (in particular the Gaussian distribution as a limit distribution). It is related to this question from which the image below is taken.

---

You can view the random walk as a diffusion process. The following steps give the rough idea

• Considered the probability distribution for the random walk to be at some point $x$ at time $t$. (consider an ensemble of many walks)

• The probability (density) $P(x,t)$ will relate to the probability at some earlier time.

  Let's for simplicity use a random walk with discrete steps in discret time. For instance, each time step the random walk takes a step $\pm 1$ with equal probability $p=0.5$. This is equivalent to taking each two time steps a step $\pm 2$ with equal probability $p=0.25$, and staying in place with probability $p=0.5$. Then

  $$P(x,t) = \underbrace{\frac{1}{4} \cdot P(x-1,t-2)}_{\substack{\text{a quarter} \\ \text{from the left}}} + \underbrace{ \frac{1}{2} \cdot P(x,t-2) }_{\substack{\text{half the value} \\ \text{from the spot $x$}}} + \underbrace{\frac{1}{4} \cdot P(x+1,t-2)}_{\substack{\text{a quarter} \\ \text{from the right}}}$$

• Or in terms of differences

  $$\begin{array}{rcl}{\nabla_t}\hphantom{^2} P(x,t) &=& P(x,t)-P(x,t-2) \\ {\nabla_x}^2 P(x,t) &=& [P(x+1,t)-P(x,t)]-[P(x-1,t)-P(x,t)]\end{array}$$

  you get

  $$\nabla_t P(x,t) = \frac{1}{4} {\nabla_x}^2 P(x,t) $$

• You could view this in the limit as a diffusion process (more specifically the heat equation)

  $$\frac{\partial}{\partial t} f(x,t) = D \frac{\partial^2}{\partial x^2} f(x,t)$$

• The normal distribution with $\sigma \propto \sqrt{t}$ satisfies the above equation process.