3

My 3rd grader studied probabilities at school. At home I decided to demonstrate how it works in practice.

So we throw a quarter 50 times. 39 was head, 11 was tail, and I miserably failed to demo half/half rule.

What would be the proper way to demonstrate how probability works for 3rd grader?

Andre Silva
  • 3,070
  • 5
  • 28
  • 55
hOff
  • 133
  • 3
  • You could use a [balance scale](https://en.wikipedia.org/wiki/Weighing_scale#Balance), and a bunch of pennies. Then flip the pennies, and put all heads on one side, all tails on the other? – GeoMatt22 Sep 28 '16 at 23:37
  • 1
    Comments: (1) Perhaps the best thing at this age is to simply play games? Games with dice etc...? Third grade math covers multiplication, division fractions? Once he/she knows that stuff, you may be able to connect with the math? (2) Something was wonky with the coin flipping because only 11 heads or fewer among 50 flips has less than a .004% chance of happening by chance. (3) Let $x$ be the number of heads, $n$ be the number of trials, and $p$ probability of flipping heads. Law of large numbers is that $\lim_{n \rightarrow \infty} \frac{x}{n} = p$ it's not $\lim_{n \rightarrow \infty} x = pn$ – Matthew Gunn Sep 29 '16 at 00:24
  • 2
    The "50:50 rule" is so often misinterpreted (e.g. as the [gambler's fallacy](https://en.wikipedia.org/wiki/Gambler%27s_fallacy)) I wonder whether it might be worth avoiding. Perhaps it's more important to get a grip on the idea that **more likely events tend to happen more often** - perhaps home-made dice, with faces reading 1, 2, 3, 6, 6, 6, might make that point? And if you wanted to introduce the fractional reasoning, you'd also see that 6 tends to turn up on about half of all rolls (once your sample size is reasonably large). – Silverfish Sep 29 '16 at 00:38
  • @Silverfish All kinds of games have non-standard dice (eg. [King of Tokyo](https://boardgamegeek.com/boardgame/70323/king-tokyo), a game strangely fun for adults too :P) – Matthew Gunn Sep 29 '16 at 00:44
  • 1
    I like the idea of dice. It is perhaps too advanced, but something like rolling a pair of dice can get at the idea of combinations, i.e. 2 = 1+1 but 4 = 2+2 or 3+1 or 1+3. – GeoMatt22 Sep 29 '16 at 00:46
  • Such an extreme result suggests you may have had a problem with the way you were tossing the coins (it's hard to bias a coin for a tossing experiment very much unless you mangle them so much they're obviously not suitable for the experiment) so I doubt the coin was the issue; that only leaves the way your organized the tossing itself (such as it not spinning very many times in the air). Such a lesson is important (for example it relates to our probability models really only applying well when the conditions are reasonably well controlled), ... ctd – Glen_b Sep 29 '16 at 01:32
  • ctd ... but perhaps that lesson comes rather earlier in the process than you hoped. What particular aspect of "how probability works" were you hoping to demonstrate? – Glen_b Sep 29 '16 at 01:32
  • There was no problem whatsoever with your demonstration: **it worked beautifully.** Not only did it illustrate the fact that outcomes can be indeterminate, it also showed one way to begin studying an indeterminate outcome (by means of frequencies) and it also showed how such a study is capable of refuting your beliefs about the world. You now have pretty strong evidence that your procedure for flipping this coin was unfair. It would be a mistake to assert the demonstration failed because the results did not agree with your beliefs: that would be a religious conclusion, not a scientific one. – whuber Sep 29 '16 at 17:31
  • @whuber, I understand that experiment I set worked well and produce results and results are well explainable from the probability theory point of view. Now, my question is, given limited number of trials (i cannot flip coins infinitely or very large number of times) what is the best way to demonstrate and explain concept of probability to 3rd grader? – hOff Sep 30 '16 at 13:39
  • That's really a question of pedagogy and psychology. Those who study such things often recommend *spinners*: usually you can find them in children's board games, constructed as cardboard circles on which is set a freely spinning dial. The circle is divided into wedges corresponding to random events. It is visually evident that the angle of each wedge is proportional to the chance of the spinner landing there. – whuber Sep 30 '16 at 14:30

1 Answers1

5

The problem with small number of tosses is that you may be inadvertently promoting avoidable fallacies. See for instance this post by Glen_b, regarding the "law of averages."

To show the law of large numbers a plot in something as available of Excel does the trick.

Here is a quick demonstration in Excel, really easy to set up. You can start off with the coin, then say something along the lines that the process is too mechanical for human consumption, and get your computer ready.

On the first column (A) generate $250$ values with RANDBETWEEN(0,1). On the adjacent column, get the cumulative average with AVERAGE($A$1:). Select the values in column B and generate a plot like this:

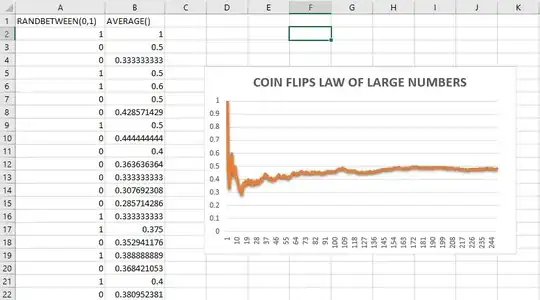
enter image description here

Make sure to emphasize that each toss is independent and completely unconnected to the prior, and to point out how far away from $0.5$ the results can be at the beginning of the experiment.

I remember the days, changing the plot, and starting with a small number of draws where the fluctuation in the plot is great. Have fun!

Community
  • 1
Antoni Parellada
  • 23,430
  • 15
  • 100
  • 197
  • Yeah, law of large numbers is that $\lim_{n \rightarrow \infty} \frac{x}{n} = p$ it's *not* the bizarre $\lim_{n \rightarrow \infty} x = pn$ (what many somehow seem to think?). The difference between the number of heads and the number of tails is essentially a random walk... it wanders off to plus or minus infinity as the number of flips goes to infinity.The law of large numbers may actually be a tricky concept for a third grader... it's actually a tricky concept for many educated adults! – Matthew Gunn Sep 29 '16 at 00:35
  • Makes sense. First do no harm! And that's quite cool that you and your kids had fun with the simulation! – Matthew Gunn Sep 29 '16 at 00:41
  • 2
    @MatthewGunn Your definitions (so concise and so critical) remind me of one of my very [favorite posts on CV](http://stats.stackexchange.com/a/159653/67822). – Antoni Parellada Sep 29 '16 at 00:51