I am trying to perform a relatively simple multiple regression with a single breakpoint using the segmented package in R. My question is how to handle the interaction between the predictor variables as follows.
My model is: $$Runoff = \beta_0+\beta_1(A+\beta_2P)$$ where there is a breakpoint at some value of $(A+\beta_2P)$. I expect $\beta_0$ and $\beta_1$ to be different on each side of the breakpoint, and $\beta_2$ to be the same (in fact I'll just say a priori that $\beta_2$ should not vary across the breakpoint, but this would be interesting to test)
My question is how to implement this using segmented (or a similar breakpoint linear regression model). Options are:
1. Run some loop through values of $\beta_2$ and create an intermediate variable $\tau = (A+\beta_2P)$, then it's a simple application of segmented. My concern is that I'd like to get a fitted value of $\beta_2$ from the data and this seems like a crude way of doing it.
2. Some clever way of using segmented on the fully explicit model that will estimate $\beta_0, \beta_1,$ and $\beta_2$
any help appreciated
ADDENDUM:
To describe what I'm trying to do. This is for a watershed runoff generation project. My hypothesis is that runoff amount is a function of both precipitation and soil water table position, and that there is a very strong threshold response in the latter. Whenever it rains, the water table goes up, but if it does not reach the threshold no runoff is generated. If enough rain falls to raise the water table above the threshold, then runoff is generated. Thus, runoff is a function of $(Ant + Pcp)$ with a notable breakpoint.
So, in the model as formulated in my original question $\beta_0$ and $\beta_1$ are the slope and intercept of the runoff response, and $\beta_2$ is a coefficient that converts rainfall depth to water table rise, which I assume is something like the porosity of the soil.
I'm interested in (in order of importance): (1) is this model better than just a linear relationship between runoff and precipitation?; (2) can the model estimate where the water table threshold is?; (3) Can the model estimate the "porosity" coefficient (this would be a nice check against physical reality and I think also improve the physical fidelity of the estimated threshold position).
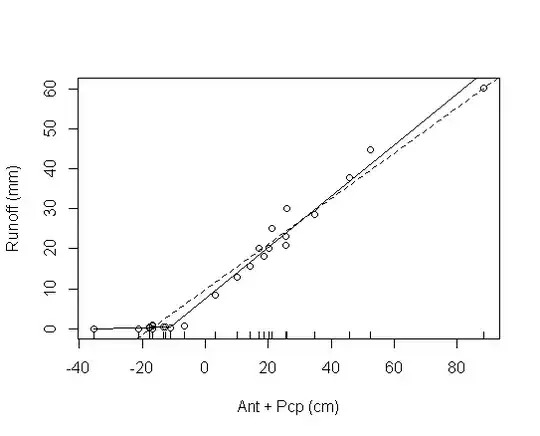
Below is a graph using a hand-picked value of $\beta_2$, which let me do a piece wise linear regression. Solid line is the piece wise, dashed is a linear regression between runoff and precip alone. I'd like to be able to estimate the parameters of the model ($\beta_0, \beta_1, \beta_2$, and the breakpoint position) from the data. Ultimately, I have three replicates of three watershed types, so I'm interested in comparisons there as well.