As I understand it, Pearsons residuals are ordinary residuals expressed in standard deviations.
I ran this Poisson regression:
library(ggplot2)
glm_diamonds <- glm(price ~ carat, family = "poisson", data=diamonds)
I then saved the Pearsons residuals and fitted values from the model:
resid <- resid(glm_diamonds, type = "pearson")
fitted <- fitted(glm_diamonds)
df <- data.frame(resid, fitted)
I then plotted the Pearsons residuals against fitted values:
ggplot(df, aes(fitted, resid)) + geom_point() + ylab("Pearsons residuals") + xlab("Fitted values")
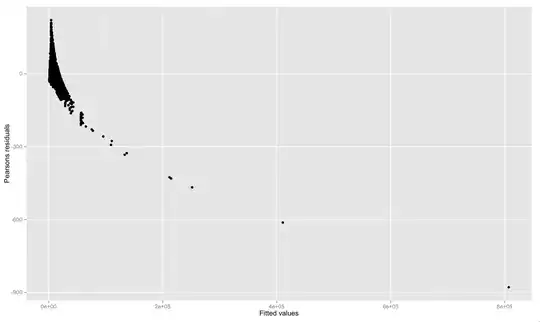
It can be seen in the plot that many of residuals are hundreds of units away from zero. If Pearsons residuals are standard deviations, why are some residuals hundreds of units away from zero? Or in other words, why don't the residuals range from about -3 to 3 if they are standard deviations?