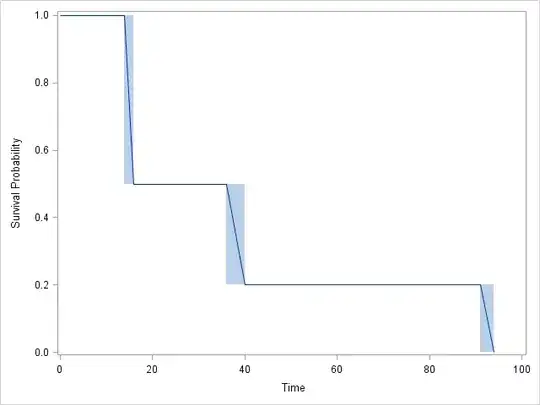
I ran an interval censor survival curve with R, JMP and SAS. They both gave me identical graphs, but the tables differed a bit. This is the table JMP gave me.
Start Time End Time Survival Failure SurvStdErr
. 14.0000 1.0000 0.0000 0.0000
16.0000 21.0000 0.5000 0.5000 0.2485
28.0000 36.0000 0.5000 0.5000 0.2188
40.0000 59.0000 0.2000 0.8000 0.2828
59.0000 91.0000 0.2000 0.8000 0.1340
94.0000 . 0.0000 1.0000 0.0000
This is the table SAS gave me:
Obs Lower Upper Probability Cum Probability Survival Prob Std.Error
1 14 16 0.5 0.5 0.5 0.1581
2 21 28 0.0 0.5 0.5 0.1581
3 36 40 0.3 0.8 0.2 0.1265
4 91 94 0.2 1.0 0.0 0.0
R had a smaller output. The graph was identical, and the output was:
Interval (14,16] -> probability 0.5
Interval (36,40] -> probability 0.3
Interval (91,94] -> probability 0.2
My problems are:
- I don't understand the differences
- I don't know how to interpret the results...
- I don't understand the logic behind the method.
If you could assist me, especially with the interpretation, it would be a great help. I need to summarize the results in a couple of lines and not sure how to read the tables.
I should add that the sample had 10 observations only, unfortunately, of intervals in which events happened. I didn't want to use the midpoint imputation method which is biased. But I have two intervals of (2,16], and the first person not to survive is failed at 14 in the analysis, so I don't know how it does what it does.
Graph: