I wish to compare two test data sets using the Mann-Whitney U and KS tests in R.
As a start, I thought to compare two similar sets (an A/A test) expecting to see a highly significant indication of similarity.
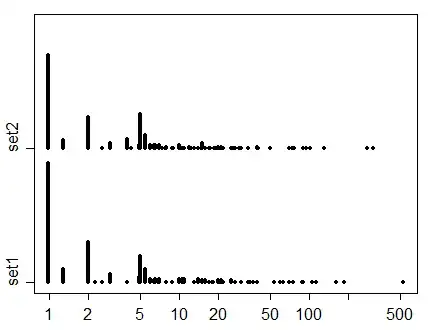
The two lists are these shown below:
https://www.dropbox.com/s/9cbvzlltdohjoef/set1.csv https://www.dropbox.com/s/1p9fqdja2khrvi1/set2.csv
The results for the Mann-Whitney U test (wilcox.test) were:
W = 22073, p-value = 0.1948
alternative hypothesis: true location shift is not equal to 0
The results for the KS test (ks.test) were:
D = 0.1021, p-value = 0.2058
alternative hypothesis: two-sided
Why are neither of these statistically significant (p-value being below 0.05)?
Here's a display of the values for the two sets: