Why is AUC higher for a classifier that is less accurate than for one that is more accurate?

Question

I have two classifiers

• A: naive Bayesian network
• B: tree (singly-connected) Bayesian network

In terms of accuracy and other measures, A performs comparatively worse than B. However, when I use the R packages ROCR and AUC to perform ROC analysis, it turns out that the AUC for A is higher than the AUC for B. Why is this happening?

The true positive (tp), false positive (fp), false negative (fn), true negative (tn), sensitivity (sen), specificity (spec), positive predictive value (ppv), negative predictive value (npv), and accuracy (acc) for A and B are as follows.

+------+---------+---------+
|      |    A    |    B    |
+------+---------+---------+
| tp   | 3601    | 769     |
| fp   | 0       | 0       |
| fn   | 6569    | 5918    |
| tn   | 15655   | 19138   |
| sens | 0.35408 | 0.11500 |
| spec | 1.00000 | 1.00000 |
| ppv  | 1.00000 | 1.00000 |
| npv  | 0.70442 | 0.76381 |
| acc  | 0.74563 | 0.77084 |
+------+---------+---------+

With the exception of sens and ties (spec and ppv) on the marginals (excluding tp, fn, fn, and tn), B seems to perform better than A.

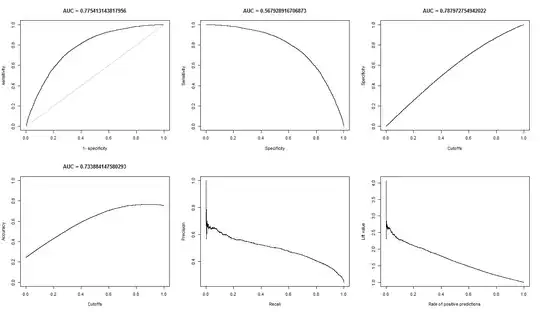
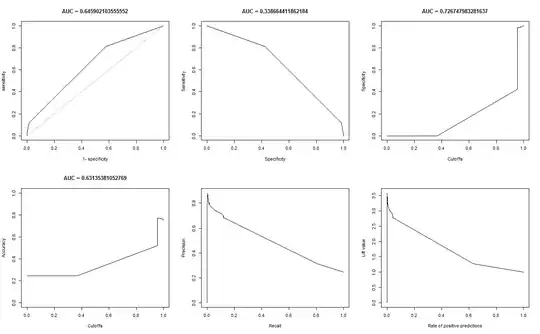
When I compute the AUC for sens (y-axis) vs 1-spec (x-axis)

aucroc <- auc(roc(data$prediction,data$labels));

here is the AUC comparison.

+----------------+---------+---------+
|                |    A    |    B    |
+----------------+---------+---------+
| sens vs 1-spec | 0.77540 | 0.64590 |
| sens vs spec   | 0.70770 | 0.61000 |
+----------------+---------+---------+

So here are my questions:

• Why is the AUC for A better than B, when B "seems" to outperform A with respect to accuracy?
• So, how do I really judge / compare the classification performances of A and B? I mean, do I use the AUC value? Do I use the acc value, and if so why?
• Furthermore, when I apply proper scoring rules to A and B, B outperforms A in terms of log loss, quadratic loss, and spherical loss (p < 0.001). How do these weigh in on judging classification performance with respect to AUC?
• The ROC graph for A looks very smooth (it is a curved arc), but the ROC graph for B looks like a set of connected lines. Why is this?

As requested, here are the plots for model A.

Here are the plots for model B.

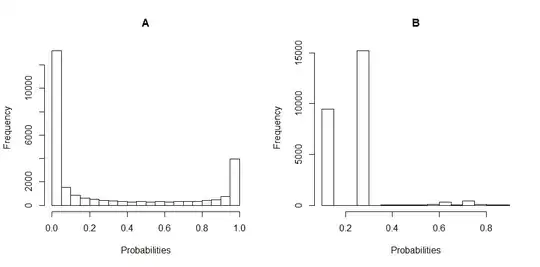
Here are the histogram plots of the distribution of the probabilities for A and B. (breaks are set to 20).

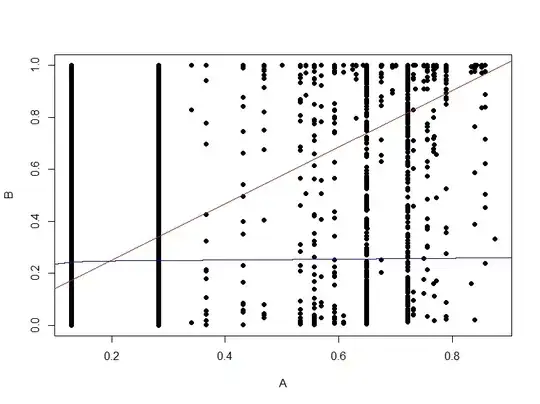
Here is the scatter plot of the probabilities of B vs A.

Answer 1

Improper scoring rules such as proportion classified correctly, sensitivity, and specificity are not only arbitrary (in choice of threshold) but are improper, i.e., they have the property that maximizing them leads to a bogus model, inaccurate predictions, and selecting the wrong features. It is good that they disagree with proper scoring (log-likelihood; logarithmic scoring rule; Brier score) rules and the $c$-index (a semi-proper scoring rule - area under ROC curve; concordance probability; Wilcoxon statistic; Somers' $D_{xy}$ rank correlation coefficient); this gives us more confidence in proper scoring rules.

Answer 2

1. Why is the AUC for A better than B, when B "seems" to outperform A with respect to accuracy?

   Accuracy is computed at the threshold value of 0.5. While AUC is computed by adding all the "accuracies" computed for all the possible threshold values. ROC can be seen as an average (expected value) of those accuracies when are computed for all threshold values.

2. So, how do i really judge/compare the classification performances of A and B? I mean, do i use the AUC value? do i use the acc value? and why?

   It depends. ROC curves tells you something about how well your model your model separates the two classes, no matter where the threshold value is. Accuracy is a measure which works well usually when classes keeps the same balance on train and test sets, and when scores are really probabilities. ROC gives you more hints on how model will behave if this assumption is violated (however is only an idea).

3. furthermore, when i apply proper scoring rules to A and B, B outperforms A in terms of log loss, quadratic loss, and spherical loss (p < 0.001). how do these weigh in on judging classification performance with respect to AUC?

   I do not know. You have to understand better what you data is about. What each model is capable to understand from your data. And decide later which is the best compromise. The reason why that happens is that there is no universal metric about a classifier performance.

4. The ROC graph for A looks very smooth (it is a curved arc), but the ROC graph for B looks like a set of connected lines. why is this?

   That is probably because the bayesian model gives you smooth transitions between those two classes. That is translated in many threshold values. Which means many points on ROC curve. The second model probably produce less values due to prediction with the same value on bigger regions of the input space. Basically, also the first ROC curve is made by lines, the only difference is that there are so many adjacent small lines, that you see it as a curve.

Answer 3

Why is the AUC for A better than B, when B "seems" to outperform A with respect to accuracy?

First, although the cut-off (0.5) is the same, it is not comparable at all between A and B. In fact, it looks pretty different from your histograms! Look at B: all your predictions are < 0.5.

Second, why is B so accurate? Because of class imbalance. In test B, you have 19138 negative examples, and 6687 positives (why the numbers are different in A is unclear to me: missing values maybe?). This means that by simply saying that everything is negative, I can already achieve a pretty good accuracy: precisely 19138 / (19138 + 6687) = 74%. Note that this requires absolutely no knowledge at all beyond the fact that there is an imbalance between the classes: even the dumbest model can do that!

And this is exactly what test B does at the 0.5 threshold... you get (nearly) only negative predictions.

A is more of a mixed bag with. Although it has a slightly lower accuracy, note that its sensitivity is much higher at this cut-off...

Finally, you cannot compare the accuracy (a performance at one threshold) with the AUC (an average performance on all possible thresholds). As these metrics measure different things, it is not surprising that they are different.

So, how do I really judge/compare the classification performances of A and B? i mean, do i use the AUC value? do i use the acc value? and why?

Furthermore, when I apply proper scoring rules to A and B, B outperforms A in terms of log loss, quadratic loss, and spherical loss (p < 0.001). How do these weigh in on judging classification performance with respect to AUC?

You have to think: what is it you really want to do? What is important? Ultimately, only you can answer this question based on your knowledge of the question. Maybe AUC makes sense (it rarely really does when you really think about it, except when you don't want to make a decision youself but let others do so - that's most likely if you are making a tool for others to use), maybe the accuracy (if you need a binary, go-no go answer), but maybe at different thresholds, maybe some other more continuous measures, maybe one of the measures suggested by Frank Harrell... as already stated, there is no universal question here.

The ROC graph for A looks very smooth (it is a curved arc), but the ROC graph for B looks like a set of connected lines. Why is this?

Back to the predictions that you showed on the histograms. A gives you a continuous, or nearly-continuous prediction. To the contrary, B returns mostly only a few different values (as you can see by the "spiky" histogram).

In a ROC curve, each point correspond to a threshold. In A, you have a lot of thresholds (because the predictions are continuous), so the curve is smooth. In B, you have only a few thresholds, so the curve looks "jumps" from a SN/SP to an other.

You see vertical jumps when the sensitivity only changes (the threshold makes differences only for positive cases), horizontal jumps when the specificity only changes (the threshold makes differences only for negative examples), and diagonal jumps when the change of threshold affects both classes.