4

What distribution does this histogram look like?

enter image description here

It doesn't seem symmetric around its mean, and it is always nonnegative and unimodal. After its mode, it seems to decay exponentially to infinity, while before its mode, it seems to increase in some different way.

How, in general, can we guess the distribution from a histogram? Are there some references or summaries for teaching me to do that? Thanks!

Tim
  • 1
  • 29
  • 102
  • 189
  • 1
    Thanks! How did you learn to know that? DO you keep a summary of these distributions, so whenever you saw a histogram, you can think of some possible distributions? – Tim Feb 22 '14 at 13:52
  • 3
    I would rather guess a distribution from a kernel density estimate, or even more than one (with different smooth). Histograms' appearance can change dramatically with different bin widths and starting points. – Peter Flom Feb 22 '14 at 13:59
  • @PeterFlom: Can I ask you the same question? How did you learn to tell from a histogram? Do you keep a summary of these distributions, so whenever you saw a histogram, you can think of some possible distributions? – Tim Feb 22 '14 at 14:17
  • I didn't follow any particular learning path; I am not that expert at this. – Peter Flom Feb 22 '14 at 14:29
  • 5
    Histograms are poor tools for estimating distributions: see http://stats.stackexchange.com/a/51753. Therefore it would be foolhardy to hazard a guess based on this one. Certain forms of summary statistics provide more powerful tools for estimating distributions. In addition to the usual (first few moments, etc.), having extreme quantiles (the quartiles, eighths, and so on) can be very helpful. The [first four moments](http://en.wikipedia.org/wiki/Pearson_distribution) alone often do a good job. – whuber Feb 22 '14 at 14:44
  • Could be gamma, chi-square, inverse gaussian, inverse beta, ... – Mike Dunlavey Feb 22 '14 at 16:29
  • It could also be [log-normally distributed](http://www.emeraldinsight.com/fig/498_10_1016_S0196-1152_07_15007-9.png) – dpastoor Feb 22 '14 at 18:25
  • Is this a sequence of independent readings or is it chronological/longitudinal ? If it is then a possible model would be the clue to characterizing the data above and beyond the first four moments. – IrishStat Feb 22 '14 at 21:53
  • @IrishStat: iid. – Tim Feb 23 '14 at 01:24
  • You can compare this histogram with [one of the 88 histograms/PDFs of these distributions](http://stackoverflow.com/a/37559471/2087463) available in a python library (`scipy.stats`) or you can [try to fit the histogram to a variety of distributions](http://stackoverflow.com/a/16651955/2087463) and see which one produces the least amount of error. – tmthydvnprt Jun 02 '16 at 14:56
  • Could be a log-normal distribution? – TrungDung Nov 19 '20 at 19:58

1 Answers1

4

1) Beware trying to assess distributional shape from a histogram with only a few bars. On occasion, you can get a misleading impression, especially if sample sizes are small. If sample sizes are big, use far more bars.

2) There are an infinite number of unimodal, slightly right skew distributions. There is no reliable way to discriminate one from any number of others.

3) Real data tends not to follow the simple distributional shapes of the common one-, two- or three- parameter distributions. Real distributions are more like heterogeneous mixtures. Simple distributional forms are convenient fictions (models, to be precise) - they approximate reality in ways that make it easier to work with.

With large samples of real data, it makes sense to work directly with the distribution you have (of which the ecdf is the sample estimate); kernel (or log-spline) density estimates give you nice smooth curves and can help you pick out modes and so on.

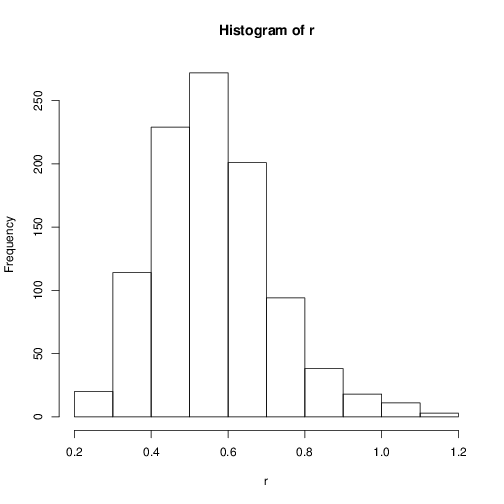
It doesn't seem symmetric around its mean, and it is always nonnegative and unimodal. After its mode, it seems to decay exponentially to infinity, while before its mode, it seems to increase in some different way.

I'd agree.

How, in general, can we guess the distribution from a histogram?

In general, you can't.

Are there some references or summaries for teaching me to do that?

Not really, since you can't really do it without narrowing the problem down (e.g. see my discussion below about how to tell a gamma from a lognormal).

What you can do is simulate many samples from distributions (at each of a number of different sample sizes) to get an idea of what they look like, and how much they can vary.

At first glance it looks like it might kind of be close to a gamma distribution.

But it might be closer to lognormal. (But it might be any of an infinity of other things, as I mentioned)

If those were the only two possibilities and I had to choose between them, I'd look at the distribution of the logs.

When you take logs, what was gamma becomes left-skew:

enter image description here

Lognormals become symmetric (obviously):

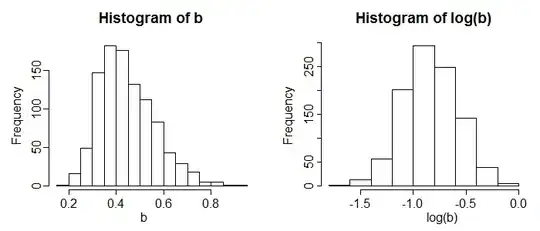
enter image description here

So that's an easy way to distinguish between those two possibilities. If it's still slightly right-skew after you take logs, I'd look at inverse gamma as one possibility.

But once you do that with actual data, don't make the mistake of thinking of your choice as anything more than a model.

(There are a number of posts here that discuss identifying distributions from histograms or Q-Q plots or kernel density estimates that make related points. Some of those are worth looking at.)

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • Thanks. By the way, the histogram is from http://stats.stackexchange.com/questions/87504/distribution-of-an-odds-ratio-under-beta-prior – Tim Feb 23 '14 at 01:26
  • 1
    Ah, but if you're in that situation, you have far more information than just the sample! It should be possible, for example, to actually compute the density function (at least numerically). – Glen_b Feb 23 '14 at 02:41
  • How do you compute the density function numerically? – Tim Feb 23 '14 at 16:58
  • That would be a whole other question, but it relates to what I was saying in comments on your other question (about convolutions of logs of scaled F distributions). So, specifically, you do numerical convolution - typically via fast Fourier transforms. Once you have the density on the log scale you can then transform the result back. – Glen_b Feb 23 '14 at 17:22
  • You can compare a histogram with [one of the 88 histograms/PDFs of these distributions](http://stackoverflow.com/a/37559471/2087463) available in a python library (`scipy.stats`) or you can [try to fit the histogram to a variety of distributions](http://stackoverflow.com/a/16651955/2087463) and see which one produces the least amount of error. – tmthydvnprt Jun 02 '16 at 15:01