Probability to draw a black ball in a set of black and white balls with mixed replacement conditions

Question

When a black ball is drawn, it is not replaced in the set, but white balls are replaced.

I have thought of this, with the notations:

• $b$, $w$ the initial number of black and white balls
• $x_i = (b - i)/(b + w - i)$

The probability of drawing a black ball $Pb(n)$ after n draws:

$$\eqalign{ Pb(0) &= x_0\\ Pb(1) &= (1-x_0)x_0 + x_0x_1\\ Pb(2) &= (1-x_0)^2x_0 + x_0x_1(1-x_0)+ x_0x_1(1-x_1) + x_0x_1x_2 \\ Pb(n) &= \sum\limits_{k=0}^{n-1} (\prod\limits_{i=0}^k x_i \prod\limits_{i<=k}^{n-k\ terms} 1-x_i) }$$

This sum seems infinite with n, even if some terms are null since $x_{i \ge b}=0$

Except $b=1$:
$Pb(n) = (1-x_0)^nx_0 $

For $b=2$:
$Pb(n)= x_0(1-x_1)^n + x_0x_1\sum\limits_{i+j=n-1} (1-x_0)^i(1-x_1)^j$

Is there a known solution to this problem?

Answer 1

Let the initial number of white balls be $w$ and black balls be $b$. The question describes a Markov chain whose states are indexed by the possible numbers of black balls $i \in \{0, 1, 2, \ldots, b\}.$ The transition probabilities are

$$p_w(i, i) = \frac{w}{w+i}, \quad p_w(i,i-1) = \frac{i}{w+i}.$$

The first describes drawing a white ball, in which case $i$ does not change, and the second describes drawing a black ball, in which case $i$ is reduced by $1$.

From now on let us drop the explicit subscript "$w$," taking this value as fixed throughout. The eigenvalues of the transition matrix $\mathbb{P}$ are

$$\mathbf{e} = \left(\frac{w}{w+b-i},\ i = 0, 1, \ldots, b\right)$$

corresponding to the matrix $\mathbb{Q}$ given by

$$q_{ij} = (-1)^{i+j+b} (j+w) \binom{b}{j} w^{j-b} \binom{b-j}{i} (b-i+w)^{b-j-1}$$

whose inverse is

$$(q^{-1})_{ij} = \frac{w^{b-i} \binom{j}{b-i} (b-j+w)^{i-b}}{\binom{b}{b-i}}.$$

That is,

$$\mathbb{P} = \mathbb{Q}\ \text{Diagonal}(\mathbf{e})\ \mathbb{Q}^{-1}.$$

Consequently the distribution after $n$ transitions out of the state $b$ is given by the vector of probabilities

$$\mathbf{p}_n = (0,0,\ldots,0,1) \mathbb{P}^n = (0,0,\ldots,0,1)\mathbb{Q}\ \text{Diagonal}(\mathbf{e}^n)\ \mathbb{Q}^{-1}.$$

That is, the chance there are $i$ black balls left after $n$ draws is

$$p_{ni} = \sum_{j=0}^b q_{nj} e_j^n (q^{-1})_{ji}.$$

For example, starting with any number of white balls and $b=2$ black balls, the probability distribution after $n \ge 1$ draws is

$$\eqalign{ \Pr(i=2) &= p_{n2} &= \frac{w^n}{(2+w)^n} \\ \Pr(i=1) &= p_{n1} &= \frac{2w^{n-1}}{(1+w)^{n-1}} - \frac{2 w^{n-1}(1+w)}{(2+w)^n} \\ \Pr(i=0) &= p_{n0} &= 1 - \frac{2 w^{n-1}}{(1+w)^{n-1}} + \frac{w^{n-1}}{(2+w)^{n-1}}. }$$

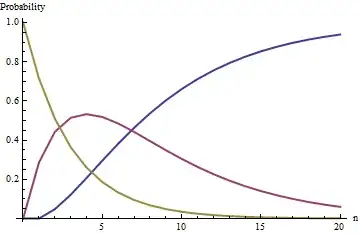
The curves in this figure track the probabilities of the states $i=0$ (blue), $i=1$ (red), and $i=2$ (gold) as a function of the number of draws $n$ when $w=5$; that is, the urn begins with two black balls and five white balls.

The state $i=0$ (running out of black balls) is an absorbing state: in the limit as $n$ grows without bound, the probability of this state approaches unity (but never exactly reaches it).