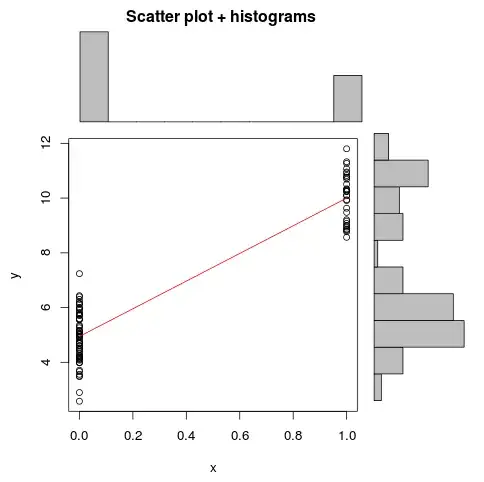
As an assumption of linear regression, the normality of the distribution of the error is sometimes wrongly "extended" or interpreted as the need for normality of the y or x.
Is it possible to construct a scenario/dataset that where the X and Y are non-normal but the error term is and therefore the obtained linear regression estimates are valid?