What kind of distribution is this "almost" uniformly distributed data for calls/week?

Question

My supervisor asked me to find out which distribution represents a particular situation.

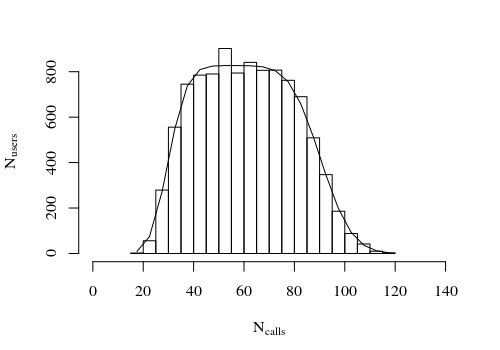
I have a VoIP generator that generates calls "uniformly" distributed between callers. This means that the volume per caller distribution is "almost" uniformly distributed between a minimum and maximum. So by running a test with 10000 users and a min value equal to 30 calls per week and a max value equal to 90 calls/week i obtain that not all the users respect this limits: we have some users that generate <30 calls and some other users that generate >90 calls. It is clear that the obtained distribution is not uniform.

The situation is this:

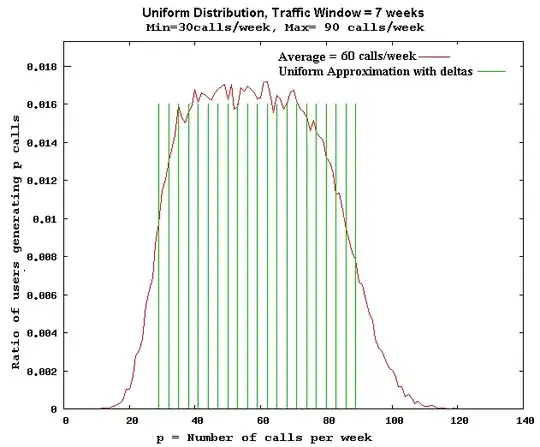
He said that i have to perform a sort of numerical process in order to find some formulas that could define this distribution. Initially, as wrote before,we wanted to obtain a uniform (min,max) distribution (the green area in the figure) but this is not the case as proved with chi-square test. Moreover the curve in figure is not symmetric, the probability of call generation below 30 call/week and greater that 90 call/week are not identical (it is high for 90calls/week). The variability of the number of generated call increases with the increasing call generation rates.

"Actually implementation of this distribution is nothing but assigning different call rates in a range for users in domain which indicates implementation of several delta functions. As the call rates increases the variability of the generated calls also increases with the average call rate and this leads to the asymmetric behavior of the curve." [cit. from the Voipgenerator documentation]

Someone can help me?I think that now i cannot use Q-Q plot because i don't know which theoretical distribution i have to use in order to compare it with my empirical data.

Sorry if I have stressed with a similar problem a few weeks ago, but initially we thought we could change the implementation, but now we cannot. Hence i have to discover the type of the distribution i obtained and i don't know how can i do this.

Answer 1

I found out that the distribution is a compound distribution of Poisson or Binomial with the uniform distribution. The steps below is how I found this out.

Use a theoretic starting point

When you are seeking for a certain distribution it is helpful to start thinking about the process that generates the data. In your case it is imaginable that a single individual will behave randomly according to some Poisson or binomial distribution with a given rate or probability which may differ from individual to individual.

Then the ensemble of all individuals can be described by a compound distribution.

Trying different models.

Initially I thought of the beta-binomial distribution which is a common distribution to model an over-dispersed binomial distribution (the function is easy to describe and there are there is lots of software/programming-language that have this standard available). However the beta-binomial was not able to model such low kurtosis.

Then I thought of a continuous distribution as the mixing distribution. A trial by mixing 21 distributions with varying parameters ($p$ between 0.5 and 1.5 times the average $p$) showed that this works well and then I worked it out more precisely by formulating the exact function and using some optimizer to fine tune the parameters.

The final model

Let $M$ be the total number of users and let $N$ be the total number of calls.

Both Poisson and binomial distributions fit your data since for small $p$ and large $N$ the $\text{Binom}(N,p)$ is nearly the same as $\text{Pois}(p*N)$. You have:

$$ X \sim \text{Binom}(N,p) \qquad \text{ or } \qquad X \sim \text{Pois}(N*p) $$

with $p$ itself being distributed according to a uniform distribution

$$p \sim \text{Unif}(0.5277 M^{-1}, 1.5186 M^{-1} ) $$

The compound distribution is

$$f_{binom*unif}(k) = \int_{p_{min}}^{p_{max}} f_{unif}(p) f_{binom}(k,p) dp $$

or

$$f_{Poisson*unif}(k) = \int_{p_{min}}^{p_{max}} f_{unif}(p) f_{Poisson}(k,Np) dp $$

which involves integrals like $\int_{p_{min}}^{p_{max}} x^a(1-x)^b dx$ or $\int_{Np_{min}}^{Np_{max}} x^ae^{-x} dx$ which can be expressed in terms of incomplete Beta and Gamma functions.

The details are, I hope, clear from the code at the end which creates the plot below showing a histogram using the data from your other question ( How to perform goodness of fit test and how to assign probability with uniform distribution? ) and superimposed a line for the calculated/fitted numbers.

library(zipfR)  # provides incomplete Beta and Gamma functions

# data
nr <- c(2,56,279,556,745,785,790,902,794,841,806,807,762,690,509,347,186,88,42,10,3)
xr <- seq(17.5, 117.5, 5)

# parameteres number of people and number of calls
m=10000
N=sum(nr*xr)

# convoluted binomial we use the logaritmic functions for thepossibly high values
Pconv = function(t, N, m, lim1=0.5, lim2=1.5) {
  bd1 <- Ibeta(x = lim1/m,
               a = t+1,
               b = N-t+1,
               log=1) 
  bd2 <- Ibeta(x = lim2/m,
               a = t+1,
               b = N-t+1,
               log=1)
  out = (m/(lim2-lim1))*(exp(lchoose(N,t) + bd2) - exp(lchoose(N,t) + bd1))
  out
}

# convoluted Possion we use the logaritmic functions for thepossibly high values
Pconv2 = function(t, N, m, lim1=0.5, lim2=1.5) {
  bd1 <- Igamma(x = lim1*N/m,
               a = t+1,
               log=1) 
  bd2 <- Igamma(x = lim2*N/m,
               a = t+1,
               log=1)
  out = (m/N/(lim2-lim1))*(exp(-lfactorial(t) + bd2) - exp(-lfactorial(t) + bd1))
  out
}

predictvalues <- function(lim1, lim2) {
  # calculate probabilities
  p <- rep(0, 151)
  for (i in 0:150) {
    p[i]<- Pconv2(i, N, m, lim1=lim1, lim2=lim2)
  }

  # cumulative p
  cdf <- cumsum(p)[-1]

  # predicted values
  npred <- m*(cdf[seq(20, 120, 5)] - cdf[seq(15, 115, 5)])  
  npred
}

# predicted values
npred <- predictvalues(0.5277, 1.5186)

# plotting
histn <- list(counts=nr,
              breaks=seq(15, 120, 5),
              mids=xr,
              xname="prediction with compound distribution",
              equidist=TRUE)
class(histn) <- "histogram"

plot(histn, xlab = expression(N[calls]), ylab = expression(N[users]), main="", xlim=c(0, 140))
lines(xr, npred, col=1, lty=1)


# finding the optimal values
nls(nr ~ predictvalues(a, b) , start=list(a=0.5, b=1.5))

Answer 2

This looks a lot like a Beta distribution from its shape and seemingly bounded domain. You can use maximum likelihood estimation to estimate the parameters $\alpha$ and $\beta$.

Answer 3

Try Q-Q plots (or P-P plots, only they are somewhat less widely used) of your empirical distribution against each of hypothetical type of distribution. The parameters for the latter are usually deduced by software from your empirical distribution although you could input parameter values you wish to check.