I have to demonstrate that a generator of VoIP calls generates calls uniformly distributed between callers. In particular the distribution is the uniform (min, max) one where the volume per caller distribution is uniformly distributed between a minimum and maximum. So by running a test with 10000 users and a min value equal to 30 calls per week and a max value equal to 90 calls/week i obtain that not all the users respect this limits.
The situation is depicted in figure:
The few users that generate <30 or >90 calls spoil the chi-square goodness of fit test and I don't know how can i proceed with a goodness of fit test. Most of the values is within the interval (and from these we obtain low chi-square value), but the few out-of-range values spoil the final chi-square calculation.
In your opinion what is the best way to operate? What should I do with the "out-of-range"values? Thank you.
PS: the chi-square goodness-of-fit test performed is reported in the following figure:
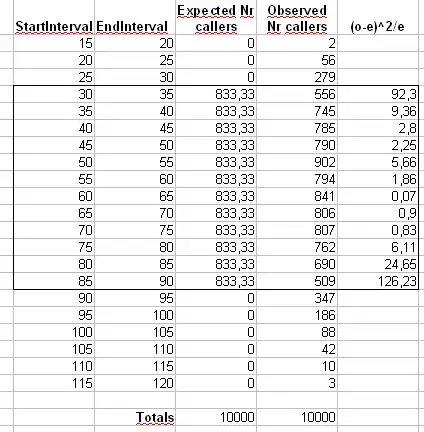
where still I don't know what to do with the out-of-range values.
UPDATE
after talking with people linked with the project we concluded that the generator does not satisfy the uniform distribution. We have to do a theoretic analysis of what we expect really to be the distribution at the end of the generation based on the inputs.
This means that I have to do it! More details: The generator assigns a "probability" between 0 and 1 to the callers (with a particular method, that probably is the problem). Then it generates a random value from 0 to 1 and it finds the associated user and assigns the call to him.
The generator generates calls for a week with the constant rate equal to 1 call per second, this means that it generates ca. 604800 total calls.
My goal is to distribute the callers between the min and max number of calls in a week. For example if I have 10000 users and the min limit is equal to 30 calls per week and max = 90 calls per week I should obtain something about:
30 calls : 163 users.
31 calls : 163 users.
....
90 calls : 163 users.
So 163 users generate 30 calls in a week..etc, etc and finally 163 users generate 90 calls in a week. How should I assign the probability to callers in order that the generator distributes the callers uniformly between the range 30-90?