All the examples of SVMs are related to classification. I don't understand how an SVM for regression (support vector regressor) could be used in regression.
From my understanding, A SVM maximizes the margin between two classes to finds the optimal hyperplane. How would this possibly work in a regression problem?
In short: Maximising the margin can more generally be seen as regularising the solution by minimising $w$ (which is essentially minimising model complexity) this is done both in the classification and regression. But in the case of classification this minimisation is done under the condition that all examples are classified correctly and in the case of regression under the condition that the value $y$ of all examples deviates less than the required accuracy $\epsilon$ from $f(x)$ for regression.
In order to understand how you go from classification to regression it helps to see how both cases one applies the same SVM theory to formulate the problem as a convex optimisation problem. I'll try putting both side by side.
(I'll ignore slack variables that allow for misclassifications and deviations above accuracy $\epsilon$)
In this case the goal is to find a function $f(x)= wx +b$ where $f(x) \geq 1$ for positive examples and $f(x) \leq -1$ for negative examples. Under these conditions we want to maximise the margin (distance between the 2 red bars) which is nothing more than minimising the derivative of $f'=w$.
The intuition behind maximising the margin is that this will give us a unique solution to the problem of finding $f(x)$ (i.e. we discard for example the blue line) and also that this solution is the most general under these conditions, i.e. it acts as a regularisation. This can be seen as, around the decision boundary (where red and black lines cross) the classification uncertainty is the biggest and choosing the lowest value for $f(x)$ in this region will yield the most general solution.
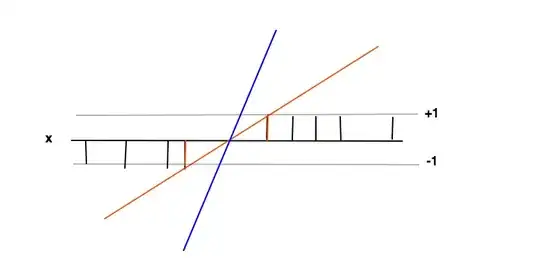
The data points at the 2 red bars are the support vectors in this case, they correspond to the non-zero Lagrange multipliers of the equality part of the inequality conditions $f(x) \geq 1$ and $f(x) \leq -1$
In this case the goal is to find a function $f(x)= wx +b$ (red line) under the condition that $f(x)$ is within a required accuracy $\epsilon$ from the value value $y(x)$ (black bars) of every data point, i.e. $|y(x) -f(x)|\leq \epsilon$ where $epsilon$ is the distance between the red and the grey line. Under this condition we again want to minimise $f'(x)=w$, again for the reason of regularisation and to obtain a unique solution as the result of the convex optimisation problem. One can see how minimising $w$ results in a more general case as the extreme value of $w=0$ would mean no functional relation at all which is the most general result one can obtain from the data.
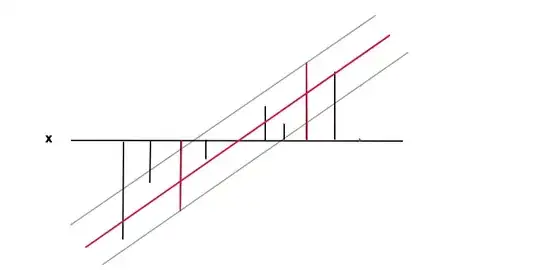
The data points at the 2 red bars are the support vectors in this case, they correspond to the non-zero Lagrange multipliers of the equality part of the inequality condition $|y -f(x)|\leq \epsilon$.
Both cases result in the following problem:
$$ \text{min} \frac{1}{2}w^2 $$
Under the condition that:
In SVM for classification problem we actually try to separate the class as far as possible from the separating line (Hyperplane) and unlike logistic regression, we create a safety boundary from both sides of the hyperplane (different between logistic regression and SVM classification is in their loss function). Eventually, having a separated different data points as far as possible from hyperplane.
In SVM for regression problem, We want to fit a model to predict a quantity for future. Therefore, we want the data point(observation) to be as close as possible to the hyperplane unlike SVM for classification. The SVM regression inherited from Simple Regression like (Ordinary Least Square) by this difference that we define an epsilon range from both sides of hyperplane to make the regression function insensitive to the error unlike SVM for classification that we define a boundary to be safe for making the future decision(prediction). Eventually, SVM in Regression has a boundary like SVM in classification but the boundary for Regression is for making the regression function insensitive respect to the error but the boundary for classification is only to be way far from hyperplane(decision boundary) to distinguish between class for future (that is why we call it safety margin).
