8

I have a question about the random walk of two kings in a 3×3 chessboard.

Each king is moving randomly with equal probability on this chessboard - vertically, horizontally and diagonally. Τhe two kings are moving independently from each other in the same chessboard. Both of them start in the same square, and then they move independently.

How could we find the probability in time $n$ both of them are in the same square, as $n$ goes to infinity?

cube
  • 143
  • 1
  • 7

3 Answers3

12

Let's exploit the symmetry to simplify the calculations.

The chessboard and its moves remain the same when the board is reflected vertically, horizontally, or diagonally. This decomposes its nine squares into three types, their orbits under this symmetry group. Correspondingly, each king can be in one of three "states": a corner square ($C$), an edge square ($E$), or the central ("middle") square ($M$). (A state ignores which particular square a king is on and tracks only its equivalence class under the group of symmetries.)

The following results are immediate:

  • From a corner square, there are two transitions to edge squares and one transition to a middle square. Because the three transitions are equiprobable,

    $$\Pr(C \to E) = 2/3,\quad \Pr(C \to M) = 1/3.$$

    This gives a row $(0, 2/3, 1/3)$ in a transition matrix for the states $(C, E, M)$.

  • From an edge square there are two transitions to corner squares, two to other edge squares, and one to the middle square. This gives a second row $(2/5, 2/5, 1/5)$ in a transition matrix.

  • From the middle square there are four transitions to corner squares and four to middle squares. The third row of a transition matrix therefore is $(4/8, 4/8, 0) = (1/2, 1/2, 0)$.

In this graph representing this Markov chain, transition probabilities are represented both by edge thickness and color:

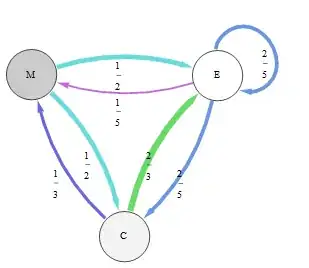
Figure

By inspection or otherwise, we find that a left eigenvector of its transition matrix

$$\mathbb{P} = \left( \begin{array}{ccc} 0 & \frac{2}{3} & \frac{1}{3} \\ \frac{2}{5} & \frac{2}{5} & \frac{1}{5} \\ \frac{1}{2} & \frac{1}{2} & 0 \\ \end{array} \right)$$

is $\omega = (3, 5, 2)^\prime$. This claim is easily checked by performing the multiplication: $\omega \mathbb{P} = 1 \omega.$ The eigenvalue manifestly is $1$. Because all states are connected, $\omega$ gives the limiting probabilities of each king being in each state; we only need to rescale its components to sum to unity:

$$\omega = (\omega_C, \omega_E, \omega_M) = (3/10, 5/10, 2/10).$$

(This is where we reap the benefits of exploiting the symmetry: instead of working with a nine by nine matrix of $81$ elements we only have to compute with a three by three matrix of $9$ elements. The reduction of the problem from nine states to three paid off quadratically by reducing the computational effort by a factor of $(9/3)^2 = 9$.)

The (limiting) chance that both kings are in a state $s$ of (limiting) probability $\omega_s$ is $\omega_s^2$ because the kings move independently. The chance that both kings are in the same cell is found by conditioning on the state: by symmetry, each cell in a given state has the same limiting probability, so if both kings are found in a state $s$ having $k_s$ cells, the chance they are both in the same cell is $1/k_s$. Whence the solution is

$$\sum_{s\in \{C,E,M\}}\frac{ \omega_s^2 }{k_s} = \left(\frac{3}{10}\right)^2\frac{1}{4} + \left(\frac{5}{10}\right)^2\frac{1}{4} + \left(\frac{2}{10}\right)^2\frac{1}{1} = \frac{9}{400} + \frac{25}{400} + \frac{16}{400} = \frac{1}{8}.$$

whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • 3
    Reader @xan makes some *very* interesting comments after the (beautiful) answer by [Accidental Statistician](http://stats.stackexchange.com/a/81634/919) in this thread. Those comments point to a logical gap in my argument: it is necessary also to show that the two kings can (in some intuitive sense) truly move independently of each other. Xan's example concerns kings that cannot make diagonal moves: if one king starts in state $E$ and the other in $C$ or $M$, then they *never* can occupy the same square! This gap can be fixed by considering a transition matrix for ordered pairs of states. – whuber Jan 09 '14 at 22:12
  • Thank you for this answer,very intresting and enlightening! – cube Jan 10 '14 at 16:32
  • @user929304 That's correct. If you imagine a different situation in which those probabilities were each (say) $1/3$, which is quite possible--their total is only $2/3$ for each king--then your formula would give a probability of $2(1/3+1/3)=4/3$ which is obviously wrong. – whuber Aug 25 '16 at 14:57
  • @user929304 The probability of the union is the sum of the probabilities only when the events are disjoint (aka "mutually exclusive"). Being disjoint is not the same as being independent--in fact, it's a rather extreme violation of independence. – whuber Aug 25 '16 at 15:15
  • @user929304 [Cox and Miller](https://books.google.com/books?hl=en&lr=&id=NeR5JEunGYwC&oi=fnd&pg=PR9&dq=david+cox+theory+%22stochastic+processes%22&ots=VbNkTFy7FE&sig=tA7mJ4yTQIpDVG4zgVgRJJajNPg#v=onepage&q&f=false) is accessible and covers a lot of ground. – whuber Sep 13 '16 at 16:05
  • @user929304 Yes, that looks possible, because the mean separation will be a function of the proportion of the time the kings are in each square, which can be computed from $\mathbb P$ alone. – whuber May 24 '17 at 13:23
10

Since the two kings are moving independently, you can consider them separately. If the board is of finite size, and doesn't have any closed subsections, this is one of those cases where the stationary distribution can be found by solving the detailed balance equation.

In this case, as $n$ goes to infinity, the probability of a king being in a square becomes proportional to the number of squares adjacent to it, i.e. three for each corner square, five for each edge square, and eight for the middle square. This sums to $40$, so the chance of being in the middle square is $8/40$, in any corner square is $3/40$, and in any edge square is $5/40$.

Since this is true for both kings independently, the chance of them both being in the middle square is $(8/40)^2 = 64/1600$, of both being in any corner square is $(3/40)^2=9/1600$, and in any edge square is $(5/40)^2=25/1600$. So the chance of them being in the same square approaches $\frac{64+4\times9+4\times25}{1600} = \frac{200}{1600} = \frac{1}{8}$ as $n$ approaches infinity.

Accidental Statistician
  • 760
  • 4
  • 14
  • Oh,your explanation is really good and i totally understand it!! – cube Jan 08 '14 at 17:34
  • Can i ask you one more think?In the last equality 1/16+8(9/1024) the numbre 8 is as result from the chessboard's dimensions?It doesn't matter that we have a 3x3 chessboard? – cube Jan 08 '14 at 17:45
  • The 8 is because I'm summing up the probabilities for each square. The outside squares all have the same probability, and there are eight of them. – Accidental Statistician Jan 08 '14 at 17:49
  • Could you please explain me about the "5 for each edge square" ? – cube Jan 08 '14 at 18:37
  • 2
    Edge squares are squares that are on the outside, but not in a corner. Each edge square has five neighbours: the middle square, two other edge squares, and two corner squares. – Accidental Statistician Jan 08 '14 at 18:41
  • Can you elaborate on "probability of being in a square becomes proportional to the number of squares adjacent to it"? Is there are rationale or a pointer to one? Is it conditional on the graph being bidirectional or other constraints? – xan Jan 09 '14 at 13:02
  • 1
    It's sufficient for the graph to be undirected (if you can move from A to B, you can move from B to A), finite (finite number of squares), and complete (no subgroup of squares from which there's no escape), and for the probability of moving in a certain direction from a square being the same for every direction. In this case, the probability of being in a square converges over time to being proportional to the number of adjacent squares. You can check this by solving either for $\pi P=\pi$ as in vinux's answer, or by solving the detailed balance equation, which is easier. – Accidental Statistician Jan 09 '14 at 14:50
  • 1
    +1 This is a pretty answer. A simple way to justify the assertion quoted by @xan is just apply the transition matrix to that vector of proportions: you will obtain the vector itself (from its very definition!), showing it is an eigenvector of eigenvalue $1$. Because all states are connected, that's the limiting distribution. (In other words, you don't actually have to solve $\pi P = \pi$; you only have to check the solution you have proposed.) – whuber Jan 09 '14 at 16:08
  • @whuber, it's a bit unintuitive that one cell's probability is not dependent on its neighbors' properties, but it is verifiable, as you say... There seems to be another condition needed to avoid cases with no steady state. For instance, if the king cannot move diagonally, he is bound to alternate black and white squares, so each cell's probability will alternate between zero and nonzero. – xan Jan 09 '14 at 19:40
  • That's the situation where the states are not connected, @xan, which is why I explicitly ruled it out. The probabilities themselves do not themselves alternate--they reach limits--but the limiting probabilities will depend on the starting states. – whuber Jan 09 '14 at 19:48
  • @whuber, they're certainly connected in some sense. That is, you can reach any state from any other state. How is "connected" defined here? I'm guessing it must mean, there exists an M such that for any N >= M, any state can reach any other state in exactly N steps. – xan Jan 09 '14 at 20:26
  • I see--I misunderstood what you said. Nevertheless, the actual alternation of black and white squares for the limited king moves is unrelated to the limiting distribution. "Connected" only means there is a positive probability of being in any particular state at some indefinite time in the future regardless of the current state. That's less stringent than your guess. BTW, for the limited king moves the answer is $17/144$, *assuming* the kings do not move in lockstep. If they do, your questioning quite validly points out an important additional consideration! – whuber Jan 09 '14 at 20:53
  • @user929304 If the next move only depends on the two kings' current positions, then yes, it should be possible to find a stable equilibrium in a similar way, and proceed from there. You'd just need to consider both kings at once, instead of separately, as I did. However, as per the discussion above between whuber and xan, you will need to check that this move dependency doesn't make it impossible for the kings to meet. – Accidental Statistician Sep 16 '16 at 17:54
  • Yes, they should. I think this agrees with what I write in the second paragraph, but we're understanding "any corner", etc., to mean different things. When I write "any corner", I'm referring to a single corner, not all four of them. – Accidental Statistician Nov 18 '16 at 00:55
6

You can solve using transition probability matrix.

$\begin{bmatrix} C_1 & C_2 & C_3 \\ C_4 & C_5 & C_6 \\ C_7 & C_8 & C_9 \\\end{bmatrix}$

Construct Transition probability matrix, using the probability of one cell to another. Eg: $P[C_1, C_2] = P[C_1, C_4]= P[C_1, C_5] = \frac{1}{3}$. P will be a $9 \times 9$ matrix.

Now you can calculate stationary probabilities (Since all states are recurrent).

Solve $\pi P = \pi $ such that $\sum \pi =1$.

This gives the probability of one king in particular square as n large. Use the independence property you can arrive at the required probability.

vinux
  • 3,429
  • 1
  • 18
  • 18