If any two variables follow a normal bivariate distribution does it also have a multivariate normal distribution?

Question

Bivariate and multivariate distribution relationship.

If we have say 3 variables where any two variables follow a normal bivariate distribution, then does it necessarily follow a multivariate normal distribution?

Answer 1

Here's a counter-example:

Let $X$, $Y$, $Z$ be independent standard normal, and let $W = |Z|\cdot \text{sign}(XY)$.

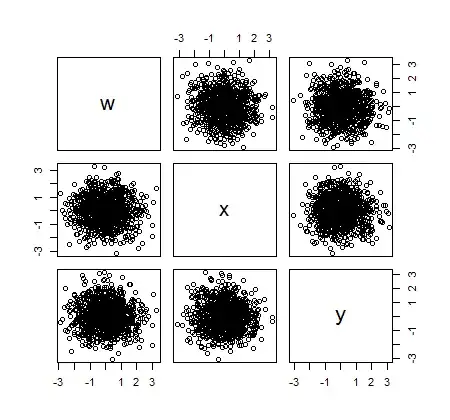
Then $(W,X)$, $(W,Y)$ and $(X,Y)$ are bivariate normal, but $(W,X,Y)$ is not trivariate normal, since $WXY$ is never negative.

What's happening is that the trivariate distribution has been constructed so that probability is only in four of the eight octants, in such a way that each quadrant of the pairwise margins gets an octant with probability and an octant without.

To help visualize what's going on, see the following simulation:

 x=rnorm(1000)
 y=rnorm(1000)
 z=rnorm(1000)
 w=abs(z)*sign(x*y)

Here are the pairwise samples:

Here's the sample bivariate distribution of $X$ and $Y$ when $W$ is restricted to be positive:

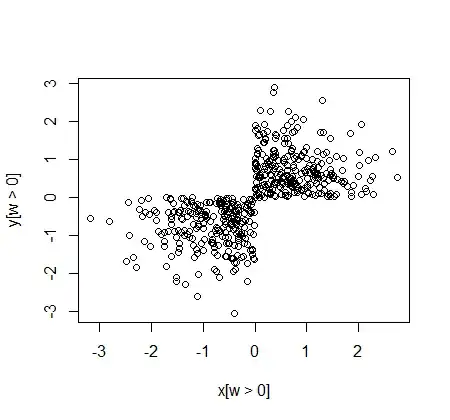
(when $W$ is restricted to be negative, the $(X,Y)$ values are in the other two quadrants)

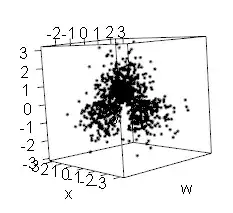
And here's a particular projection of the trivariate distribution; you should, for example, be able to make out that there's a low-density "gap" at the bottom.

---

That might seem like a somewhat artificial counterexample, but it's not an issue just with some odd edge-cases. More generally, the trivariate distribution may be quite different from trivariate normal, in any number of smooth or not-smooth ways. The same goes for more than three variables.

Copulas give us a way of constructing infinities of such counterexamples with various characteristics.

Answer 2

No. In theory, exceptions like @Glen_b's answer may apply.

In practice, multivariate normality partly depends on how precisely your variables follow their normal uni/bivariate distributions. It is rare that any real distribution has exactly zero skewness and zero excess kurtosis, after all. Therefore, if you're inferring that all the bivariate distributions are normal because you fail to reject the null hypothesis of a multivariate normality test on each, the result of the same test for all three variables might just cross your rejection threshold if the bivariate results are all $p = .06$ and your $\alpha = .05$. This answer may not matter to you if you've already avoided such problems with significance tests of normality though, and have determined through better means that your variables are normally distributed (whether exactly, or close enough).

Even so, in practice, one may find that subsets of data exhibit problematic relationships like that in Glen_b's example. Acceptable deviation from bivariate normality, once mixed with even limited instances of such multivariate problems, may exceed your purpose's tolerance for non-normality, which is bound to appear to some extent in most real sample data.