Is there a situation in which the mean of a Y variable is not 0 (e.g. not standardized), but we would still fit a regression model without intercept?
It would yield a worse fitting model, so is there a scenario in which you would omit adding an intercept with a good reason?
The intercept in a linear regression model may represent two totally different things:
A) Your theoretical model may lead you to a specification with a constant term. A basic example from Economics is when one wants to estimate the parameters of a production function (a statistical relationship that links output produced with production factors used)
$$Q = AK^aL^b$$ where $Q$ is output, $K$ is capital used and $L$ is labor used. $A$ is a shift factor, representing "technology", assumed constant in the short-run. To linearize this model we take the logs of the variable and we arrive at
$$\ln Q = \ln A +a\ln K + b\ln L$$
Including an error term we have an econometric linear regression specification -and the constant estimates $\ln A$.
B) But even if your theory does not account for a constant term, widespread advice with observational data at least, is not to omit the constant, except if you are "very sure" about the omission (and this advice holds for logistic regression too, by the way). Why such an advice? Because the existence of a constant absorbs the possibly non-zero mean of the error term.
This is a recognition that our model may not include all factors that affect/are associated with the dependent variable. What we do "hope" is that any variable omitted is independent (or at least uncorrelated) with the included regressors. But even if these omitted variables are indeed independent/uncorrelated, they still create a non-zero mean for the dependent variable (which is incarnated as a non-zero mean of the error term), around which the dependent variable fluctuates with the included regressors. By including the constant, we capture this mean value (perhaps together with a constant factor that is postulated by our model), and we can make the assumption that the expected value of the error term (usually conditional on the included regressors), is zero, which we need for various results to pass through.
This fact, that the constant term may essentially be the sum of totally different things, is what makes us in many cases not to try to interpret it.
Regarding the logistic regression, the constant term reflects the (negative of) the possibly non-zero threshold of the latent continuous variable above which the binary dependent variable becomes unity -so again, its inclusion permits us to "safely" specify an error term with conditional zero mean.
As several others have already mentioned, there are many situations where theory dictates a regression through the origin (e.g. y = corn production, x = amount of cultivated land; when x=0, y must be 0). In these situations, I would first run a traditional regression with a constant and slope term. Then, test whether the estimated intercept is significantly different than zero (Kutner, 2004). If the intercept is not significantly different than zero anyways, you may have a good argument for setting it equal to zero.
NOTE: What happens if you KNOW the function must go through the origin, but you still have a significant intercept term? Beware of the following scenario:
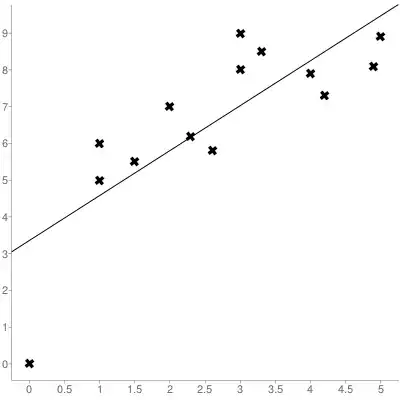
Here, the data point in the lower left corner corresponds to (0,0). Nevertheless, the linear regression appears to have a significant, positive, intercept. The underlying reason is likely that, between $x=0$ and $x=1$, there is a rapid, non-linear increase in $Y$. That is, the linear model is a good approximation for the data within $x \geq 1$, but does not extrapolate well below this range. This can suggest further refinements to your model.
WARNING: As Alecos explained, the residuals in a regression through the origin model will typically have a nonzero mean and will not sum to zero. Why is this important? The short answer is that it affects the calculation of $R^2$, and can make it difficult to interpret. In fact, $R^2$ can be negative in this case.
To see this, we have to consider how $R^2$ is derived. We start with the identity:
$$(Y_i - \bar{Y}) = (Y_i - \hat{Y}_i) + (\hat{Y}_i - \bar{Y})$$
where $\bar{Y}$ is the mean of all dependent variable observations $Y_i$, and $\hat{Y}_i$ is our predicted value for each observation. Now square both sides and sum over all $i$:
$$\sum(Y_i - \bar{Y})^2 = \sum(Y_i - \hat{Y}_i)^2 + \sum(\hat{Y}_i - \bar{Y})^2 + 2 \sum(Y_i - \hat{Y}_i)(\hat{Y}_i - \bar{Y})$$
It can be shown that, for a linear model with a slope and intercept, the cross-product term is equal to zero. However, this is not the case for regression through the origin. If that term did go to zero, we get the following equation
$$\sum(Y_i - \bar{Y})^2 = \sum(Y_i - \hat{Y}_i)^2 + \sum(\hat{Y}_i - \bar{Y})^2$$
which states that the total variability in the dependent variable, $SSTO = \sum(Y_i - \bar{Y})^2$, is the sum of the variability explained by the model, $SSR = \sum(\hat{Y}_i - \bar{Y})^2$, and the remaining unexplained variability $SSE = \sum(Y_i - \hat{Y}_i)^2$. We summarize this with the $R^2$ statistic, $R^2 = SSR/SSTO$.
However, all of this is based on the assumption that $\sum(Y_i - \hat{Y}_i)(\hat{Y}_i - \bar{Y})=0$. Again, this is not the case for regression through the origin. In extreme cases, when $SSR>SSTO$, $R^2$ will be less than zero.
References: The following article succinctly describes all of this: Eisenhauer (2003) "Regression through the Origin". Also see the textbook "Applied Linear Regression Models" by Kutner et al. (I believe chapter 3 has a section devoted to this).
Edit: After posting I came across this previous question, which is very relevant. Removal of statistically significant intercept term increases $R^2$ in linear model
