Why is functional form so important when specifying models?

Question

Variables:
lprice = log(price of house)
ldist = log(distance from incinerator)
lintst = log(distance from interstate)

1st regression

2nd regression:

In the 2nd regression I included lintstsq, which is the squared lintst from the 1st regression, and suddenly ldist and lintst become significant and their coefficients change. This doesnt make sense, how come the statistical package couldnt pick up that lintst was significant until I included its squared form, lintstsq? Can someone provide insight into this?

My lecturer's comment on this was:

This makes sense. Being close to the interstate is useful, especially for commuters who use the interstate to get to work. But being too close is not good owing to the noise and pollution. If distance from the incinerator site and distance to the interstate are correlated, we need to get the model specification with respect to the latter right in order to identify the effect of the former.

which doesnt help explain much(or does it?)

Answer 1

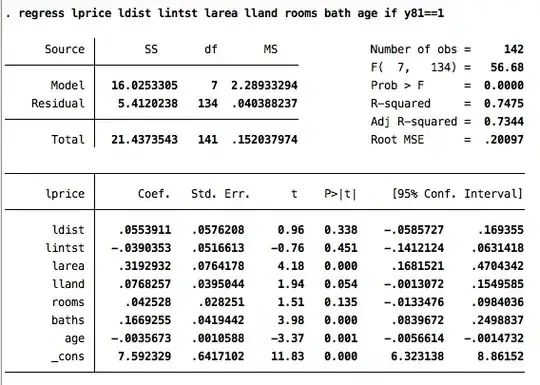
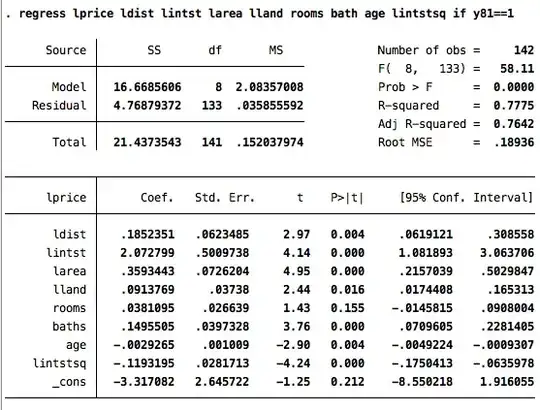
In a regression, when we include a variable in its level and in its square, and when the coefficient on the level is positive while the coefficient on the square is negative, then we are looking at a non-monotonic relation that has a maximum point (which is what your lecturer alluded too by "being close is good due to commotion facilitation but being too close is not good due to noise and pollution").

Consider a usual deterministic function

$$y= ax^2 + bx$$

The 1st derivative of the function is $$\frac {\partial y}{\partial x} = 2ax + b = 0 \Rightarrow x^* = \frac {b}{-2a}$$

If $b>0$ and $a<0$ (as happens in your regression) then $x^* >0$ and $\frac {\partial^2 y}{\partial x^2} = 2a <0$ so the critical point is a maximum: so there is an optimal distance from the interstate, $x^*$, regarding house prices: further away the costs from longer commotion time outweigh the benefits of reduced noise/pollution while if closer the costs of increased noise/pollution outweigh the benefits of reduced commotion time: so the effect on house prices is not monotonic. Graphically think of it as an "inverted u".

Now if the relation is indeed like that, then consider what happens when you only include the level and not the square: the model tries to match an actual "Up and then Down" relation to a straight line (which is what you permit the model by including only the level). Then for some range (left to the maximum) the model finds an upward sloping "straight line" (positive direction/coefficient), while for some other ranges (to the right of the maximum) the model finds a downward sloping "straight line" (negative direction/coefficient) -and this is exactly what the model tells you: "statistically insignificant" means that the coefficient may be either positive or negative (look at the confidence interval).

Two notes:
a) Work out how the above translate in your case where the variables are log-transformed.
b) I would worry about the sudden large switch in the sign, value, and statistical significance of the constant term.