2

Accidentally, I found (by simulation) that the range of a normally distributed sample is related to the estimator of the standard deviation:

$$X \sim \mathcal{N}\left(\mu, \sigma\right)$$

$$s(X) = \frac{1}{3}\left(\max(X) - \min(X)\right)$$

Why is that? I can't find any references. Is it related to the three sigma rule?

Germaniawerks
  • 1,027
  • 1
  • 10
  • 15
  • (i) You'll have to give more context about exactly what you did. (ii) the distribution of the actual [ratio of range to sd](http://en.wikipedia.org/wiki/Studentized_range) changes with sample size. [relevant post](http://stats.stackexchange.com/questions/69575/relationship-between-the-range-and-the-standard-deviation) – Glen_b Dec 23 '13 at 22:31
  • You can apply the same math that produces the 3-sigma rule. For a total range of 3 standard deviations, you're looking at the density within $\pm 1.5\sigma$, which you can calculate to be about 0.87 (http://www.wolframalpha.com/input/?i=CDF%5BNormalDistribution%5B0%2C1%5D%2C1.5%5D-CDF%5BNormalDistribution%5B0%2C1%5D%2C-1.5%5D). So by the logic of the 3-sigma rule, 87% of your data "should" lie in that range, and not 100% of it. I didn't want to put this as an answer because it doesn't really answer the question. Can you replicate the result with a different seed? – shadowtalker Dec 23 '13 at 23:28
  • I generated 10 000 samples of size 50 from standard normdist. Then observed the distribution of sample ranges. Applied sqrt transform. I got means varying around 3. As the variance and stdev of normdists was 1, hence the ratio of range(x)/3. Such ratio must have a limit anyway for any finite variance distribution. – Germaniawerks Dec 23 '13 at 23:39
  • Why are you taking square roots there? – Glen_b Dec 24 '13 at 11:10
  • To reduce the skew. – Germaniawerks Dec 24 '13 at 11:52

2 Answers2

2

There are two possibilities here: scaling the sample range to get an approximate idea of the sample standard deviation, and using the sample range to produce an estimate of the population $\sigma$ (my earlier comment failed to make the distinction clear).

I think your question is asking about the second, but I'll deal with both.

I'll tackle these two in order.

The ratio of sample range ($\max(x) - \min(x)$) to sample standard deviation is sometimes call the studentized range.

So if the middle of the distribution of studentized range was 3, it could make sense to approximate the sample standard deviation from the range by dividing the range by 3.

[Some people are no doubt wondering why we'd bother - after all why not just calculate the standard deviation instead of a noisy approximation of it? Perhaps we're trying to an eyeball estimate from a scatterplot or something, and the range is relatively quick to get by eye. Sometimes we can get the minimum and maximum but not the standard deviation.]

So for the normal distribution, how is the studentized range distributed?

Here are simulated distributions, for 100000 simulations at various sample sizes for normal data:

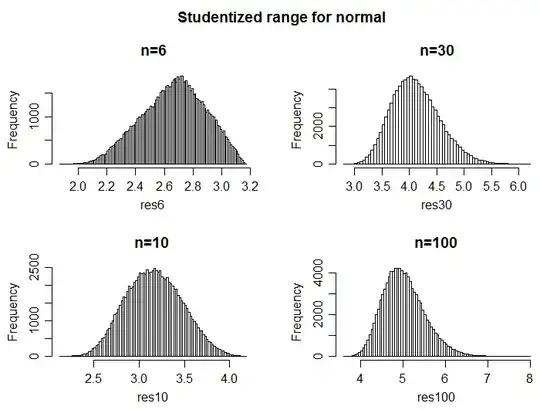
enter image description here

         mean        sd
n=6   2.663658 0.2198905
n=10  3.164088 0.3085827
n=30  4.119035 0.4355710
n=100 5.025396 0.4884935

If instead we're trying to estimate the population standard deviation, what matters is the distribution of the range at $\sigma=1$ (since we can work out the distribution for other $\sigma$ is obtained by direct scaling):

enter image description here

          mean        sd
n=6   2.536377 0.8495843
n=10  3.080769 0.8013887
n=30  4.088134 0.6918155
n=100 5.016027 0.6044998

This results in somewhat different distributional shape and different mean and standard deviation (though Slutsky's theorem suggests that as $n$ becomes large they should be more and more similar).

-

The answers to this question discusses the interesting property that at n=6, for many different distributions the range divided by 2.5 provides a reasonable approximation to the standard deviation.

Tippett produced extensive tables of the expected value of the sample range for the standardized normal in 1925 (and briefer tables of the standard deviation and standardized 3rd and 4th moments).

Tippett, L.H.C. (1925),
On the Extreme Individuals and the Range of Samples Taken from a Normal Population,
Biometrika 17 (3-4): 364-387

In either case (approximating $s$ or estimating $\sigma$ for samples from normal distributions), around sample sizes of 8-9, dividing by 3 produces a reasonably good estimate.

In very large samples, you'd expect a kind of 6-sigma rule to apply, since the "3-sigma" rule is 3 standard deviations either side of the mean. But it's not an asymptotic result since in sufficiently large samples you expect to see the range exceed $6\sigma$. Indeed, by n=1000, we're already close to $6.5\sigma$, and by n=10,000 its near $7.7\sigma$, and for n=100,000 it's somewhere above $8.75\sigma$; the mean of the distribution of the range continues to increase as $n$ increases, but at what appears to be roughly as the square-root of the log of the sample size (that's a pretty slow increase). (Edit indeed, it seems that it's been known for a long time that the growth in mean range is asymptotically proportional to $\sqrt{\log n}$)

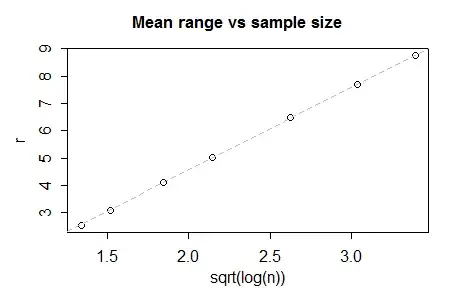
enter image description here

Update based on discussion in comments:

It sounds from your comments that the distribution of values are actually reasonably right skew.

I just did a quick simulation to see (at sample size 100) what gamma shape parameter would result in a typical ratio of (max-mean)/(mean-min) of around 1.76 (it turns out to be about $\alpha=7$). So then the question is, for that shape, and at that sample size, how much difference does it make if you use the normal values above?. The somewhat surprising answer is 'hardly any at all'.

You'd want to check at some other sample sizes, but the upshot is - if the actual distribution of values on which your extremes and mean are based is a shifted gamma with shape parameter around 7 (which is moderately skew) - then, at least near n=100, estimates of $\sigma$ you produce from scaling max-min as if they were normal should be about right.

That surprises me that it had even this level of robustness, but it should reassure you a little, at least.

Having repeated the simulation exercise at n=30, and a shape parameter of 7, if the ratio of (max-mean)/(mean-min) doesn't tend to be much larger than 1.76, you should be pretty safe - at least on average - using that normal-based rule to estimate $\sigma$ if the distribution of results isn't much heavier tailed than gamma.

Community
  • 1
Glen_b
  • 257,508
  • 32
  • 553
  • 939
  • You are right, the ratio is not constant. I'm going around this because I have a situation where there are only sample size, mean and max, min records for each empirical distribution, while they are supposed to be normal. Therefore I need to find a good estimate for StDev from those. – Germaniawerks Dec 24 '13 at 10:32
  • Ok, now I have: studentized range=3*sqrt(ln(n))-1.45 where n>2 – Germaniawerks Dec 24 '13 at 10:54
  • If you know it's normal, then you can use an equation like that (though `-1.513 + 3.0341 * sqrt(ln(n))` looks more accurate to me). If it isn't normal, you have a problem because the distribution of the range can vary a lot across differing distribution of the data. The knowledge of the mean might allow you to get a better estimate of the standard deviation if you assume a *particular* skewed distribution (such as a shifted gamma, perhaps). – Glen_b Dec 24 '13 at 11:08
  • Ok, although it should be normal, it's slightly right skewed in fact, I suspect, as the midrange is always right of the mean. Now how can I get the best estimate of StDev knowing the sample size, mean, max and min? – Germaniawerks Dec 24 '13 at 11:35
  • This is much more tricky. You would need to make some assumptions (akin to the normal assumption), but it sounds like there's little basis to make any. There are an infinite number of mildly right skew distributions. I mentioned the possibility of a shifted gamma already, but the estimates will be very sensitive to small changes in the extremes. If there was any more information it might make a difference. Are the minimums always positive? Generally close to zero? Are there any of these subsets for which you actually know the standard deviation, or indeed any other information? – Glen_b Dec 24 '13 at 15:50
  • If we were to estimate it from max-mean and mean-min separately, there'd be two different estimates which would presumably tend to lie above and below (respectively) the symmetric max-min -based estimates we've been discussing. The larger of the two (presumably max-mean) would tend to be an over-estimate and the smaller an under-estimate (as might be the one based on the range). Some kind of combined measure would presumably do reasonably well, one that would tend to combine the information in some way but leave you between (or tend to) the estimates based on the range and the max-mean...(ctd) – Glen_b Dec 24 '13 at 16:01
  • (ctd) ... but if the distribution were actually lighter tailed than normal, it may be that all three estimates are too high! – Glen_b Dec 24 '13 at 16:02
  • The data is poisitive and the minima are distant from zero. It is the average fuel consumption per 100km of many drivers driving a car with specific parameters. – Germaniawerks Dec 24 '13 at 16:02
  • Useful information! A shifted gamma might do well enough (but so might a shifted lognormal, or a Weibull, ... or any number of other possibilities, and all will produce different answers). One nice thing about a shifted gamma is that sums and averages should also be shifted gamma. Are there typical $n$'s? Or are they all over the place? – Glen_b Dec 24 '13 at 16:08
  • What do you mean by typical n's? – Germaniawerks Dec 24 '13 at 16:10
  • The sample sizes from which the max, min, mean are calculated. Oh, and what's the typical size of the ratio of max-mean to mean-min? – Glen_b Dec 24 '13 at 16:11
  • The (max-mean)/(mean-min) ratio is about 1.76 and sample sizes are various from tens to hundreds. – Germaniawerks Dec 24 '13 at 16:17
  • If you generally see that much difference (from a ratio of 1) in a sample size of hundreds, you really are unlikely to be close to normal. What is the standard deviation being used for? – Glen_b Dec 24 '13 at 16:22
  • The coefficent of variation and confidence interval for those means. – Germaniawerks Dec 24 '13 at 16:26
  • Okay. If you can say, what are those pieces of information being used for? – Glen_b Dec 24 '13 at 16:33
  • please see my updated answer (added information at the end) – Glen_b Dec 24 '13 at 17:27
  • Thanks. Then I suppose I can use the formula based on the plot in your answer (studentized range vs. sqrt(ln(n))) to estimate standard deviations. – Germaniawerks Dec 25 '13 at 18:34
  • Well, my simulation only checked the gamma-distribution case at a particular sample size (for a parameter value that had a good chance of reproducing that 1.76 figure). I can look at some other sample sizes, and possibly other distributions. Hold on... Have now done n=30; it's also fine. – Glen_b Dec 26 '13 at 04:15
0

I don't think this can be correct. The range of a normal random variable is $(-\infty, \infty)$, hence $\lim\limits_{n\rightarrow \infty} min\{X_1...X_n\} = -\infty$ and $\lim\limits_{n\rightarrow \infty} max\{X_1...X_n\} = \infty$. However, your denominator remains constant at 3, so this estimator will diverge as your sample gets larger, and is hence inconsistent. This has nothing to do with the three sigma rule.