49

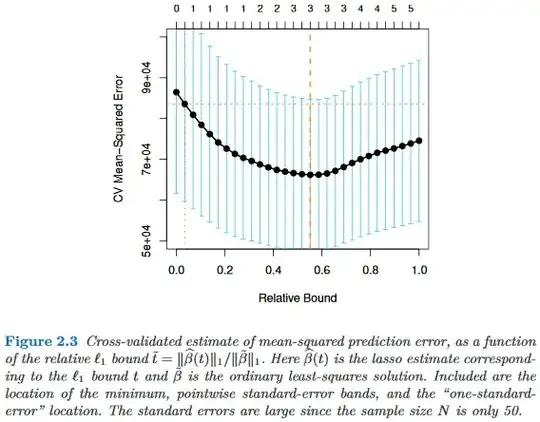
Are there any empirical studies justifying the use of the one standard error rule in favour of parsimony? Obviously it depends on the data-generation process of the data, but anything which analyses a large corpus of datasets would be a very interesting read.

The "one standard error rule" is applied when selecting models through cross-validation (or more generally through any randomization-based procedure).

Assume we consider models $M_\tau$ indexed by a complexity parameter $\tau\in\mathbb{R}$, such that $M_\tau$ is "more complex" than $M_{\tau'}$ exactly when $\tau>\tau'$. Assume further that we assess the quality of a model $M$ by some randomization process, e.g., cross-validation. Let $q(M)$ denote the "average" quality of $M$, e.g., the mean out-of-bag prediction error across many cross-validation runs. We wish to minimize this quantity.

However, since our quality measure comes from some randomization procedure, it comes with variability. Let $s(M)$ denote the standard error of the quality of $M$ across the randomization runs, e.g., the standard deviation of the out-of-bag prediction error of $M$ over cross-validation runs.

Then we choose the model $M_\tau$, where $\tau$ is the smallest $\tau$ such that

$$q(M_\tau)\leq q(M_{\tau'})+s(M_{\tau'}),$$

where $\tau'$ indexes the (on average) best model, $q(M_{\tau'})=\min_\tau q(M_\tau)$.

That is, we choose the simplest model (the smallest $\tau$) which is no more than one standard error worse than the best model $M_{\tau'}$ in the randomization procedure.

I have found this "one standard error rule" referred to in the following places, but never with any explicit justification:

amoeba
  • 93,463
  • 28
  • 275
  • 317
DavidShor
  • 1,281
  • 1
  • 11
  • 18
  • 7
    Although I know what you're referring to by "One Standard Error Rule", I strongly suspect that a lot of people won't, but would be interested in this question if they did. Maybe you could edit to add a couple of explanatory sentences? (Just a suggestion...) – jbowman Dec 21 '13 at 00:41
  • 2
    @jbowman: I just edited the question to explain the one standard error rule, bumping it since I'm also pretty interested in this... and the answer below does not really answer my questions. Anyone, please feel free to improve. – Stephan Kolassa Apr 09 '15 at 14:52
  • Related: http://stats.stackexchange.com/questions/138569 – amoeba Feb 06 '17 at 20:59
  • 2
    It would make a nice topic for a paper. It seems like a sensible engineering heuristic, but not all SEHs work in practice, so a study over a large number of datasets would be interesting. I do wonder if there is a multiple hypothesis testing issue involved that may mean it isn't very well calibrated, but it I would have thought it would be better than doing nothing on datasets where this sort of over-tuning is likely to be a problem. The question is does it make performance much worse on datasets where it isn't an issue? – Dikran Marsupial Feb 11 '17 at 13:45

3 Answers3

20

For an empirical justification, have a look at page 12 on these Tibshirani data-mining course notes, which shows the CV error as a function of lambda for a particular modeling problem. The suggestion seems to be that, below a certain value, all lambdas give about the same CV error. This makes sense because, unlike ridge regression, LASSO is not typically used only, or even primarily, to improve prediction accuracy. Its main selling point is that it makes models simpler and more interpretable by eliminating the least relevant/valuable predictors.

Now, to understand the one standard error rule, let's think about the family of models we get from varying $\lambda$. Tibshirani's figure is telling us that we have a bunch of medium-to-high complexity models that are about the same in predictive accuracy, and a bunch of low-complexity models that are not good at prediction. What should we choose? Well, if we're using $L_1$, we're probably interested in a parsimonious model, so we'd probably prefer the simplest model that explains our data reasonably well, to paraphrase Einstein. So how about the lowest complexity model that is "about as good" as all those high complexity models? And what's a good way of measuring "about as good"? One standard error.

Paul
  • 9,773
  • 1
  • 25
  • 51
  • 2
    I don't get the logic of this answer. E.g.: "unlike ridge regression, LASSO is not a mechanism for improving prediction accuracy" - why? Why is L1 so different from L2? In the next sentence you describe what happens with L1 for low lambdas, but I think the same things happens with L2 for low lambdas. – amoeba Feb 12 '17 at 22:48
  • At a high level, the L1 penalty behaves like a subset selector. Higher lambda values reduce the subset, lower lambda values expand it. Below a certain lambda value, nothing is excluded and it's basically unregularized regression with a bit of weak shrinkage. The models below this threshold are all about the same in predictive performance. It's also true that L2 regularized regression becomes more like unregularized regression as lambda decreases, but there's no specific lambda value that marks any kind of transition. – Paul Feb 13 '17 at 00:22
  • 2
    Note that this is a heuristic explanation and relies on some unstated assumptions, like all predictors are informative. If you have a ton of noise predictors and a few informative ones, there might indeed be a value of lambda which clearly and markedly optimizes the CV metric: the one that corresponds to selecting the subset of informative predictors. As lambda decreases below that value you're just letting noise in and hurting the model. – Paul Feb 13 '17 at 00:25
  • What if there are many hyper parameters, is there a corresponding one-standard error rule? – KevinKim Mar 27 '17 at 15:06
  • Not really - it wouldn't be that helpful because the one standard error rule is only a single constraint and can only uniquely determine a single hyperparameter. At best, you could create a pareto frontier of simplest models that are within one standard error of the optimal CV, and choose a model from that frontier. – Paul Mar 27 '17 at 15:28
  • @amoeba looking back on this answer and your comment, I think your point is well-taken and I've amended the answer to instead emphasize how L1 is sold (as a parsimony-promoting mechanism) and how that naturally leads L1 users to want a rule like this. It's still speculative, but in the absence of an answer from Tibshirani himself, I think it's the best-supported speculation. – Paul Mar 27 '17 at 15:41
  • Thanks Paul. My concern is that you present an argument for why 1-standard-error-rule could make sense for lasso *as opposed to* ridge, but my impression was that Hastie+Tibshirani recommend using this rule for ridge regression too (or at least for elastic net with any value of lasso/ridge ratio). – amoeba Mar 27 '17 at 20:08
  • 1
    I think the argument works equally well for ridge and lasso, if you use a broad definition of parsimony in which more regularization -> simpler model. However, it's easier to motivate for L1 than for L2 due to the different types of problems and datasets they are used on. People who use L1 are more interested in having a simple model, and they are more likely to encounter the kind of CV error curve exhibited by Tibshirani. – Paul Mar 27 '17 at 20:19
  • 1
    From the classic [ESL](http://statweb.stanford.edu/~tibs/ElemStatLearn/printings/ESLII_print10.pdf) text, p. 224: "Often a “one-standard error” rule is used with cross-validation, in which we choose the most parsimonious model whose error is no more than one standard error above the error of the best model." The example given is subset regression and a knee-shaped curve vs. number of predictors is shown. The curve is flat above the correct # of predictors, which is again consistent with the explanation I've given above. No rigorous or mathematical justification is mentioned. – Paul Mar 28 '17 at 17:37
  • 1
    So I think the main issue here is that the minimum is poorly determined, but the most-regularized model within one sigma of the minimum is well-defined. – Paul Mar 28 '17 at 17:49
18

The following is not an empirical study, which is why I originally wanted to post it as a comment, not an answer - but it really turns out to be too long for a comment.

Cawley & Talbot (J of Machine Learning Research, 2010) draw attention to the difference between overfitting during the model selection phase and overfitting during the model fitting phase.

The second kind of overfitting is the one most people are familiar with: given a particular model, we don't want to overfit it, i.e., to fit it too closely to the particular idiosyncrasies of the single data set we typically have. (This is where shrinkage/regularization can help, by trading a small increase in bias against a large decrease in variance.)

However, Cawley & Talbot argue that we can overfit just as well during the model selection stage. After all, we still have typically only a single data set, and we are deciding between different models of varying complexity. Evaluating each candidate model in order to select one usually involves fitting that model, which can be done using regularization or not. But this evaluation in itself is again a random variable, because it depends on the specific data set we have. So our choice of an "optimal" model can in itself exhibit a bias, and will exhibit a variance, as depending on the specific data set from all data sets we could have drawn from the population.

Cawley & Talbot therefore argue that simply choosing the model that performs best in this evaluation may well be a selection rule with small bias - but it may exhibit large variance. That is, given different training datasets from the same data generating process (DGP), this rule may select very different models, which would then be fitted and used for predicting in new datasets that again follow the same DGP. In this light, restricting the variance of the model selection procedure but incurring a small bias towards simpler models may yield smaller out-of-sample errors.

Cawley & Talbot don't connect this explicitly to the one standard error rule, and their section on "regularizing model selection" is very short. However, the one standard error rule would perform exactly this regularization, and take the relationship between the variance in model selection and the variance of the out-of-bag cross-validation error into account.

For instance, below is Figure 2.3 from Statistical Learning with Sparsity by Hastie, Tibshirani & Wainwright (2015). Model selection variance is given by the convexity of the black line at its minimum. Here, the minimum is not very pronounced, and the line is rather weakly convex, so model selection is probably rather uncertain with a high variance. And the variance of the OOB CV error estimate is of course given by the multiple light blue lines indicating standard errors.

one standard error rule

Community
  • 1
Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
  • This is an interesting perspective (+1). Here on CV @dikranmarsupial (one of the authors of this paper) has mentioned overfitting-during-model-selection many times in many excellent answers. But my impression was that selecting a regularization parameter $\lambda$ is one case where such overfitting would actually tend to be small if not negligible (in contrast to selecting across vastly different models). See e.g. his answer here http://stats.stackexchange.com/a/178347. – amoeba Feb 06 '17 at 16:22
  • @amoeba: thanks for that link! I wasn't aware of [@dikranmarsupial's writing about overfitting during model selection](http://stats.stackexchange.com/search?q=overfitting+model+selection+user%3A887) - serves to show I should spend more time on CV than reading papers ;-) I agree that this is probably a bigger problem for larger/higher dimensional model spaces than the one-dimensional lasso case. – Stephan Kolassa Feb 06 '17 at 16:27
  • 1
    Haha, [try this search](http://stats.stackexchange.com/search?tab=votes&q=cawley%20talbot%20user%3a887) (or put a hyphen in your query). – amoeba Feb 06 '17 at 16:31
  • Yes, the fact that we can overfit during model-selection is exactly why just picking the $\lambda$ that maximizes out of sample performance will tend to pick $\lambda$ too large. We could evaluate just how large with nested cross-validation. – Andrew M Feb 07 '17 at 17:18
  • 3
    If you only have one regularisation parameter, then that sort of over-fitting tends not to be too problematic (as the optimisation problem only has one degree of freedom), but if you have many regularisation parameters (e.g. automatic relevance determination for neural nets) then it can quickly end up being very substantial. The one sd method is a nice heuristic for avoiding over-optimising the regularisation parameter, but it would be nice to try and have something with a bit more justification (1/2) – Dikran Marsupial Feb 11 '17 at 13:29
  • 2
    The two approaches that we (Mrs Marsupial and I) have investigated is to regularise the hyper-parameters with a hyper-hyper-parameter that is integrated out analytically (http://jmlr.csail.mit.edu/papers/volume8/cawley07a/cawley07a.pdf) or to convert some of the hyper-parameters into parameters and fit them directly to the data as well, at the expense of adding an extra regularisation parameter (but that still reduces the degrees of freedom for model selection, so it still helps) (http://theoval.cmp.uea.ac.uk/publications/pdf/nn2014a.pdf) (2/2) – Dikran Marsupial Feb 11 '17 at 13:33
  • 2
    Incidentally, over-fitting in model selection can result in the model over-fitting *or* under-fitting the training set, which can make the problem a bit more tricky to diagnose. From a Bayesian perspective, the best thing to do is not to optimise, but to marginalise over $\lambda$, but that is computationally expensive or tricky or both. A big advantage of the 1sd rule is that it is at the other end of that spectrum, and being an engineer, I like simple things that work ;o) (3/2) – Dikran Marsupial Feb 11 '17 at 13:37
  • 1
    One thread about optimizing-lambda-vs-marginalizing-over-lambda topic that @DikranMarsupial mentioned is http://stats.stackexchange.com/questions/24799. That discussion is about ridge regression, and marginalizing is probably (?) trickier for lasso / elastic net / etc, whereas the beauty of CV is that it's so easy to implement. – amoeba Feb 12 '17 at 15:53
  • 1
    @amoeba for the lasso regulariser, it is possible to integrate out the regularisation parameter analytically, leaving a hyper-parameter free problem (e.g. http://theoval.cmp.uea.ac.uk/publications/pdf/nips2006a.pdf and https://academic.oup.com/bioinformatics/article/22/19/2348/240686/Gene-selection-in-cancer-classification-using but the idea is from Peter Williams, who used the same approach for automatically pruning neural networks). It doesn't work well for every dataset, but it is a useful approach for multinomial models with many $\lambda$ parameters to tune. – Dikran Marsupial Feb 13 '17 at 07:55
  • 1
    @DikranMarsupial Thanks, very interesting. Can one do it for the L1+L2 elastic net? – amoeba Feb 13 '17 at 08:14
  • 1
    I expect so, although I am not aware of any paper where it has been done. The same integrate-out approach was used for an L2 penatly for neural nets by (IIRC) Buntine and Wiegend (although I found it doesn't work as well as William's L1 penalty in the case of MLPs), so you should be able to try the same approach for both penalty terms (I think I used the integrated-out L2 penatly when regularising the kernel parameters and that worked pretty well). Trouble with Bayesian approaches is they tend to be sensitive to model mis-specification in a way CV is not, so CV still useful! – Dikran Marsupial Feb 13 '17 at 08:18
3

The number of variables selected by the Lasso estimator is decided by a penalty value $\lambda$. The larger is $\lambda$, the smaller is the set of selected variables. Let $\hat S(\lambda)$ be the set of selected variables using as penalty $\lambda$.

Let $\lambda^ \star$ be the penalty selected using the minimum of the cross validation function. It can be proved that $P(S_0 \subset \hat S(\lambda^\star))\rightarrow 1$. Where $S_0$ is the set of the variables that are really non 0. (The set of true variable is content strictly in the set estimated using as penalty the minimum of the cross-validation.)

This should be reported in Statistics for high dimensional data by Bühlmann and van de Geer.

The penalty value $\lambda$ is often chosen through cross-validation; this means that with high probability too many variables are selected. To reduce the number of selected variables the penalty is increased a little bit using the one standard error rule.

amoeba
  • 93,463
  • 28
  • 275
  • 317
Donbeo
  • 3,001
  • 5
  • 31
  • 48
  • 1
    Can you go into a bit more detail here? This seems fascinating. – DavidShor Apr 09 '14 at 21:07
  • 1
    *this means that with high probability too much variables are selected.* -- to me it is not obvious why, and why with high probability too *few* variables could not be selected. After all, cross-validated selection should give an estimate of $\lambda$ that has little bias but probably high variance, as noted in the answer by Stephen Kolassa. – Richard Hardy Feb 12 '17 at 14:27
  • I think the fact is that selecting more variables than required will reduce the prediction performance less than selecting not enough variables. For this reason CV tends to select more variables. – Donbeo Feb 12 '17 at 14:53
  • have a look at this book http://www.springer.com/gp/book/9783642201912 and to the lasso chapter here https://drive.google.com/open?id=0B3FIuCA5bZUaT2ZLWFBIZ1JYbHM – Donbeo Feb 12 '17 at 15:58
  • This is the book I meant – Donbeo Feb 12 '17 at 22:19
  • If I understood your argument correctly, it hinges on $\subset$ sign not being $\subseteq$ in the formula $P(S_0 \subset \hat S(\lambda^\star))\rightarrow 1$. Are you sure it's not $\subseteq$? – amoeba Feb 12 '17 at 22:45
  • it was a long time ago so I do not remember the details but the strict subset is reported on page 16 of the linked book. I am quiet sure that what I wrote in the answer is correct. – Donbeo Feb 12 '17 at 22:53
  • Yes, but non-strict subset is on page 18 (I only skimmed through now, without reading in detail)... – amoeba Feb 13 '17 at 20:37
  • I think you need an additional condition such as the irrepresentable condition in order to have the non-strict inclusion. Have a look for example to the example 3.2 of the paper "Stability Selection" by Buhlmann and Meinshausen – Donbeo Feb 13 '17 at 21:10
  • I see no indication from any of the linked books and mentioned papers that the subset is meant to be strict. The ⊂ sign typically means ⊆ in mathematical papers and the results involved aren't strong enough to prove anything strict. For example in Bühlmann and van de Geer, there is no way that (2.9) can be used to prove a strict form of (2.11). Nor does Example 3.2 in the paper cited above get us anywhere near such a general result; and anyway, the problem cited in that example seems to occur irrespective of the value of lambda, so is irrelevant in this context. – Paul Mar 27 '17 at 16:30
  • I think the intuition here is correct but I'd bet a large sum there's no mathematical proof of strict containment to back it up. The mathematical tools needed to do something like that are simply not in evidence anywhere in the presented materials. – Paul Mar 27 '17 at 16:58
  • I haven't look at this for a long time but I think that if the irrepresentable condition is not met then you always have the strict inclusion. – Donbeo Mar 27 '17 at 17:00
  • @RichardHardy: the CV performance estimate is subject to (at least) 2 sources of variance: A the uncertainty in performance estimation of each tested surrogate model due to the limited (finite, small) number of tested cases and B variance between the true performance of the surrogate models, i.e. model instability. B increases with overfitting, i.e. increasing model complexity. Which means (particularly if many models are compared) that the overall risk of encountering a model that accidentally looks much better than the average model at that complexity increases with increasing overfitting. – cbeleites unhappy with SX May 17 '18 at 18:56
  • 1
    With underfitting, there is no corresponding increase in variance that could accidentally compensate the average loss in performance. So all in all, you run a certain risk to pick a too complex model, but a much lower risk to pick a too simple model. Together, you get a bias in direction of too complex models. – cbeleites unhappy with SX May 17 '18 at 18:57
  • @cbeleites, very interesting, that might be just what I was missing. Thank you! Now having re-read Stephen Kolassa's answer I think he means roughly the same. – Richard Hardy May 17 '18 at 19:31