LASSO: selection of penalty term: "one-standard-error" rule

Question

I'm studying LASSO regression, in particular the choice of the optimal tuning parameter.

The glmnet package and the book "Elements of Statistical Learning" offer two possible tuning Parameters: The $\lambda$, that minimizes the average error, and the $\lambda$, selected by the "one-standard-error" rule.

I couldn't find any research or evidence on

1. the "one-standard-error" rule, and
2. which $\lambda$ I should use for my LASSO-regression.

EDIT: From the textbook elements of statistical learning

"Often a “one-standard error” rule is used with cross-validation, in which we choose the most par- simonious model whose error is no more than one standard error above the error of the best model."

Answer 1

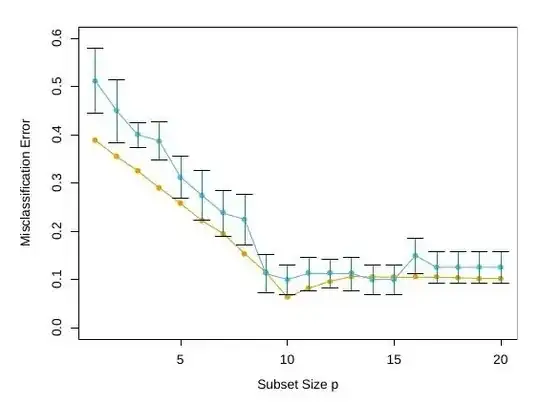
I don't know of any rigorous justification for the "one-standard-error" rule. It seems to be a rule of thumb for situations where the analyst is more interested in parsimony than in predictive accuracy.

It's important to recognize the artificial model being evaluated in the section of ESL that brings up the "one-standard-error" rule (p.244; Figure 7.9 posted by @Rickyfox) and how that type of model might not be relevant to many real-world problems. It's "from the scenario in the bottom right panel of Figure 7.3," which is explained in text on p. 226: it's a classification problem with 80 cases. The 20 predictors are each uniformly and independently distributed in [0,1]; the true class is 1 if the sum of the first 10 predictors is > 5.

Thus the model used for this example has no correlations among the predictors, and 10 of the predictors have no predictive value at all. If you didn't know beforehand how many predictors are associated with the class membership but you suspected that only a small number are and that the predictors wouldn't be inter-correlated, one could argue that the "one-standard-error" rule would tend to give you the smallest useful LASSO model, and would be close to the "true" model.

I haven't, however, come across many real-world situations where there are no correlations among the predictors or where one could a priori assume that a large number are unrelated to outcome. In those cases I don't know that there is any justification for the "one-standard-error" rule. Minimum cross-validation error would seem much better justified in such real-world situations.

Also, note that the variable selection performed by LASSO makes the most sense in situations where there aren't correlations among predictors. If there are such correlations, the specific predictors selected are likely to depend heavily on the data sample at hand, as you can illustrate by repeating LASSO on multiple bootstrapped samples of such a dataset. So, yes, you can select predictors with LASSO but there is no assurance, with correlated predictors, that the selected predictors are in any sense "true" predictors, just useful ones.

Answer 2

Regarding your first question:

The authors use this figure on p. 244 to illustrate what they mean with 'one-standard-error' rule.

Standard error bars are shown, which are the standard errors of the individual misclassification error rates for each of the ten parts. Both curves have minima at p = 10, although the CV curve is rather flat beyond 10. Often a “one-standard error” rule is used with cross-validation, in which we choose the most parsimonious model whose error is no more than one standard error above the error of the best model. Here it looks like a model with about p = 9 predictors would be chosen, while the true model uses p = 10.

As they state in the last sentence, the minimum of the CV error is at p=10 (while it looks like being the same at p=14 and p=15). Since in this example a smaller parameter value results in a more general model, they end up selecting the smallest parameter value whichs error is less than one standard error larger than the 'true optimum'.
With the error bars plotted in the graph, you can see that the error of p=9 still lies withing the error of p=10 (look at the upper 'antenna'), while the even more general model with p=8 has an error that exceeds that.

Regarding your second question:

The selection of hyperparameters is always delicate. If you have data that you can set aside to perform model selection via cross-validation as detailed in the section of the text book, then this is a reasonable approach.

You can examine how your model performs with different $\lambda$ values and plot them in a similar fashion, then decide based on the results. The rule mentioned above gives you a straight-forward directive on which value to select in the end.

Answer 3

To answer the second part of your question:

Robert Tibshirani (who introduced the Lasso) writes in "introduction to statistical learning" on the subject of tuning parameter selection:

Cross-validation provides a simple way to tackle this problem. We choose a grid of λ values, and compute the cross-validation error for each value of λ ... We then select the tuning parameter value for which the cross validation error is smallest.

The advised way seems to be to search for the optimal value for your problem with the use of cross-validation.