Why does the ACF of an AR(1) contains sometimes a sinusoid-like pattern? and what does it mean?
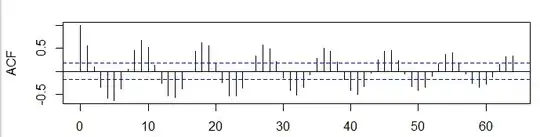
EDIT
I think the time series is fit to AR(1). As I understand it, in an AR model, the value of x at time t is a linear function of the value of x at time t–1.
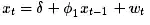
If wt is random, then we see a random Figure in correlogram. If not, we can see a pattern in correlogram, is it correct? If yes why do we see here a sinusoid pattern? In this case has the wt (Residual) a constant value?