13

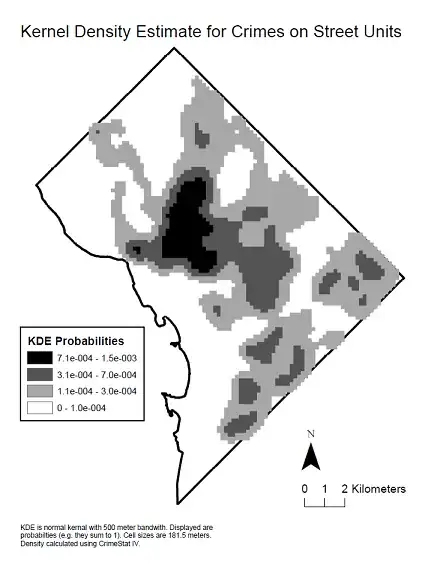
I've noticed in my own work this pattern when examining a spatial correlogram at varying distances a U-shaped pattern in the correlations emerges. More specifically, strong positive correlations at small distance bins decrease with distance, then reach a pit at a particular point then climb back up.

Here is an example from the Conservation Ecology blog, Macroecology playground (3) – Spatial autocorrelation.

Moran's I Correlogram

These stronger positive auto-correlations at larger distances theoretically violate Tobler's first law of geography, so I would expect it to be caused by some other pattern in the data. I would expect them to reach zero at a certain distance and then hover around 0 at further distances (which is what typically happens in time series plots with a low order AR or MA terms).

If you do a google image search you can find a few other examples of this same type of pattern (see here for one other example). A user on the GIS site has posted two examples where the pattern appears for Moran's I but does not appear for Geary's C (1,2). In conjunction with my own work, these patterns are observable for the original data, but when fitting a model with spatial terms and checking the residuals they do not appear to persist.

I haven't come across examples in time-series analysis that display a similar looking ACF plot, so I'm unsure of what pattern in the original data would cause this. Scortchi in this comment speculates that a sinusoidal pattern may be caused by an omitted seasonal pattern in that time series. Could the same type of spatial trend cause this pattern in a spatial correlogram? Or is it some other artifact of the way that the correlations are calculated?

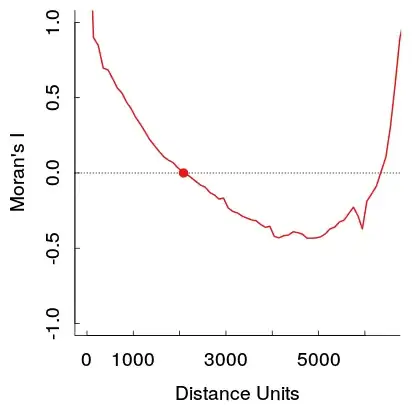
Here is an example from my work. The sample is quite large, and the light grey lines are a set of 19 permutations of the original data to generate a reference distribution (so one can see the variance in the red line is expected to be fairly small). So although the plot is not quite as dramatic as the first one shown, the pit and then rise at further distances appear pretty readily in the plot. (Also note the pit in mine is not negative, as is the other examples, if that materially makes the examples different I do not know.)

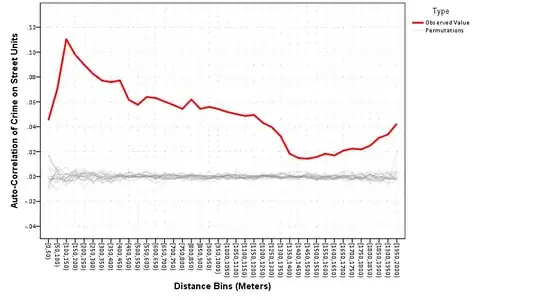
enter image description here

Here is a kernel density map of the data to see the spatial distribution that produced said correlogram.

KDE Crime in DC

Community
  • 1
Andy W
  • 15,245
  • 8
  • 69
  • 191
  • 2
    I'm not sure if this is correct, so I'm not posting it as an answer, but my guess would be that at smaller distances, very few observations are near by, and the ones that are are highly similar. At modest distances, more observations become "nearby", but they are less similar, so the effect washes out. At large distances, everything is nearby, so large but distant effects drive $I$ back up. (High-five for studying my hometown, btw.) – Sycorax Jun 02 '14 at 19:41
  • I can see where that is coming from @user777, although I might expect a similar argument that would cause the plot to trend to 0 as asymptotically the spatial neighborhood gets larger. That is, as the neighborhood grows bigger, the neighborhood mean is going to be closer to the grand mean. In my head (I think) that would make the correlation go towards zero, not one though, but I could be easily wrong. (The same argument should apply to time series as well, and I don't remember seeing any ACF plots for time series that look like this though.) – Andy W Jun 02 '14 at 19:52
  • The kde of DC reminds me a bit of a chessboard. What would the spatial autocorrelation plot from a chessboard look like? I wonder if it wouldn't be high at close distances (same square), low a little further out (different square), & then higher again. I don't know enough about this topic to know if that's the answer, though. – gung - Reinstate Monica Jun 02 '14 at 19:59
  • @gung, it depends on how you formulate distance in that case. For a [checkerboard with queen contiguity](http://stats.stackexchange.com/a/100888/1036) it would be synonymous to a negative auto-regressive term, which for a time-series would cause an ACF plot to be alternative between positive and negative correlations (and the wave would dampen, likely very quickly in that case). It is more complicated though in spatial analysis than in time series. I wouldn't characterize this pattern as a checkerboard though. – Andy W Jun 02 '14 at 20:06
  • 2
    Your data set really doesn't have enough spatial coverage that you should be estimating autocovariances at a distance of 5 kilometers (the whole area isn't much more than 10 kilometers across and you generally want to have a data set that covers many times the correlation length.) It appears to me that you've got basically three "blobs" of high crime in roughly a triangular shape, with the blobs about 5K apart from each other and gaps in between. Thus it isn't surprising to see positive correlation at that length. – Brian Borchers Jun 02 '14 at 21:55
  • @BrianBorchers - the first graph is not mine, it is from another study I used to illustrate the same pattern. My study correlogram plot is the second one, and only ranges 2,000 meters (I agree it is not meaningful to estimate longer distances). I have plenty of data, I use crime aggregated to street midpoints and intersections over D.C., in total it is 21,506 units (and I stopped at 2,000 meters because it is quite a chore, to estimate the correlogram for that far took 11 million pair-wise comparisons). – Andy W Jun 03 '14 at 12:03
  • My guess is that the density around the edges is correlated with itself. – shadowtalker Jul 06 '14 at 15:08
  • I'm not quite sure what you mean @ssdecontrol - care to elaborate? – Andy W Jul 06 '14 at 15:11
  • I don't know much about spatial econometrics but it seems like the blobs are about 2km wide, so the white space around the edges is going to correlate with itself. Not sure if that's how it works. – shadowtalker Jul 06 '14 at 15:55

1 Answers1

5

Explanation

A u-shaped correlogram is a common occurrence when its calculation is carried out across the full extent of the region in which a phenomenon occurs. It shows up particularly with plume-like phenomena in nature, such as localized contamination in soils or groundwater or, as in this case, where the phenomenon is associated with a population density which generally decreases towards the boundary of the study area (the District of Columbia, which has a high-density urban core and is surrounded by lower-density suburbs).

Recall that the correlogram summarizes the degree of similarity of all data according to their amount of spatial separation. Higher values are more similar, lower values less similar. The only pairs of points at which the greatest spatial separation can be achieved are those lying at diametrically opposite sides of the map. The correlogram therefore is comparing values along the boundary to each other. When data values tend overall to decrease toward the boundary, the correlogram can only compare small values to small values. It likely will find them to be very similar.

For any plume-like or other spatially unimodal phenomenon, therefore, we can anticipate before ever collecting the data that the correlogram will likely decrease until about half the diameter of the region is reached and then it will begin to increase.

A secondary effect: estimation variability

A secondary effect is that there are more data point-pairs available to estimate the correlogram at short distances than at longer distances. At medium to long distances, the "lag populations" of such point pairs decrease. This increases the variability of the empirical correlogram. Sometimes this variability alone will create unusual patterns in the correlogram. Evidently a large dataset was used in the top ("Moran's I") figure, which reduces this effect, but nonetheless the increase in variability is evident in the larger amplitudes of local fluctuations in the plot at distances beyond 3500 or so: exactly half the maximum distance.

A long standing rule of thumb in spatial statistics therefore is to avoid computing the correlogram at distances greater than half the diameter of the study area and to avoid to using such great distances for prediction (such as interpolation).

Why spatial periodicity is not the full answer

The literature on spatial statistics indeed notes that spatially periodic patterns can cause a rebound in the correlogram at larger distances. The mining geologists call this the "hole effect." A class of variograms that incorporate a sinusoidal term exists in order to model it. However, these variograms all impose some strong decay with distance, too, and therefore cannot account for the extreme return to full correlation shown in the first figure. Moreover, in two or more dimensions it is impossible for a phenomenon to be both isotropic (in which the directional correlograms are all the same) and periodic. Therefore periodicity of the data alone will not account for what is shown.

What can be done

The correct way to proceed in such circumstances is to accept that the phenomenon is not stationary and to adopt a model that describes it in terms of some underlying deterministic shape--a "drift" or "trend"--with additional fluctuations around that drift which may have spatial (and temporal) autocorrelation. Another approach to data like the crime counts is to study a different related variable, such as crime per unit population.

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • Thank you, do you think some ad-hoc weighting for edge effects is called for? (That may be overkill for exploratory analysis of model residuals.) My dissertation I am actually using non-linear spatial drift and trend terms - crime per unit population is annoying for multiple reasons. The residential population isn't really the baseline of interest - it is more like the walking around population. Inner city areas this can swell by alot (20~30 times) during certain hours and is more related to non-residential institutions (work and entertainment). – Andy W Jul 06 '14 at 16:25
  • You have a lot of choices, Andy, because there is no way to identify a unique model: you need to decide where you want to stop modeling the values in terms of a spatial drift and start modeling them (or rather, their residuals) with a stochastic spatial model. The u-shaped correlogram can be understood as a strong indication that *some* mechanism of modeling the drift is needed. Normalizing by a relevant population (even if it can only be grossly estimated) is one method available to you. Including measures of population (or use, etc.) as covariates is another. – whuber Jul 06 '14 at 22:07
  • I've come close using just a wide set of measures of activity land use (bars, gas stations, hospital, schools, etc.) plus the spatial terms. Here is the map of the predictions holding those other [covariates constant](https://dl.dropboxusercontent.com/s/kx6ozxnc095277c/SurfacePredictions%28Mean%29.png). There is still a tiny bit of residual auto-correlation though. I'm skeptical given the error how much dasymetric mapping of the population to small places will help, but I imagine I will undertake that analysis eventually. – Andy W Jul 07 '14 at 12:20
  • That's a principled approach: let theory guide the development of the drift component of the model and then evaluate the residuals to decide whether it would be worth the trouble of modeling their spatial autocorrelation. In many cases most of the apparent spatial relationships are adequately explained by drift terms and it is rare to need the full geostatistical machinery. One intriguing aspect of your problem is that the underlying metric (spatial distance) arguably should be travel time or travel distance *along the street network* rather than Euclidean distance. – whuber Jul 07 '14 at 15:03