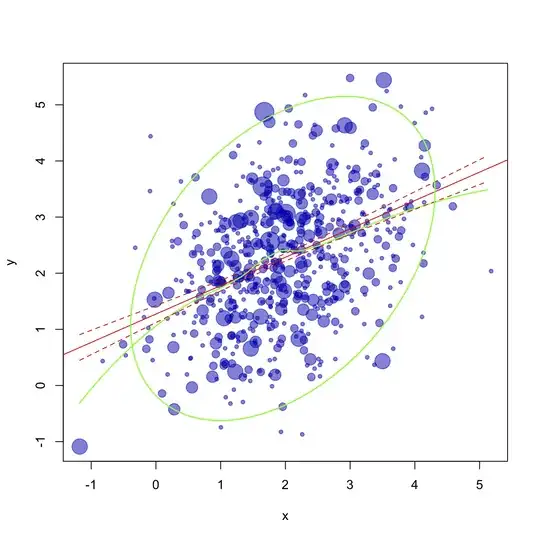
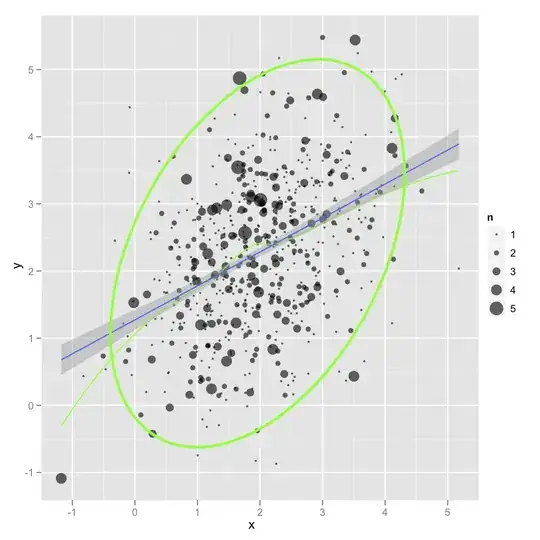
I need to draw a complex graphics for visual data analysis. I have 2 variables and a big number of cases (>1000). For example (number is 100 if to make dispersion less "normal"):
x <- rnorm(100,mean=95,sd=50)
y <- rnorm(100,mean=35,sd=20)
d <- data.frame(x=x,y=y)
1) I need to plot raw data with point size, corresponding the relative frequency of coincidences, so plot(x,y) is not an option - I need point sizes. What should be done to achieve this?
2) On the same plot I need to plot 95% confidence interval ellipse and line representing change of correlation (do not know how to name it correctly) - something like this:
library(corrgram)
corrgram(d, order=TRUE, lower.panel=panel.ellipse, upper.panel=panel.pts)
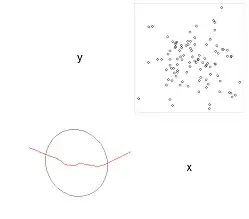
but with both graphs at one plot.
3) Finally, I need to draw a resulting linar regression model on top of this all:
r<-lm(y~x, data=d)
abline(r,col=2,lwd=2)
but with error range... something like on QQ-plot:
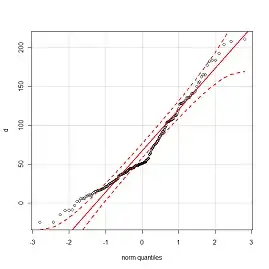
but for fitting errors, if it is possible.
So the question is:
How to achieve all of this at one graph?