I am learning R and have been experimenting with analysis of variance. I have been running both
kruskal.test(depVar ~ indepVar, data=df)
and
anova(lm(depVar ~ indepVar, data=dF))
Is there a practical difference between these two tests? My understanding is that they both evaluate the null hypothesis that the populations have the same mean.
There are differences in the assumptions and the hypotheses that are tested.
The ANOVA (and t-test) is explicitly a test of equality of means of values. The Kruskal-Wallis (and Mann-Whitney) can be seen technically as a comparison of the mean ranks.
Hence, in terms of original values, the Kruskal-Wallis is more general than a comparison of means: it tests whether the probability that a random observation from each group is equally likely to be above or below a random observation from another group. The real data quantity that underlies that comparison is neither the differences in means nor the difference in medians, (in the two sample case) it is actually the median of all pairwise differences - the between-sample Hodges-Lehmann difference.
However if you choose to make some restrictive assumptions, then Kruskal-Wallis can be seen as a test of equality of population means, as well as quantiles (e.g. medians), and indeed a wide variety of other measures. That is, if you assume that the group-distributions under the null hypothesis are the same, and that under the alternative, the only change is a distributional shift (a so called "location-shift alternative"), then it is also a test of equality of population means (and, simultaneously, of medians, lower quartiles, etc).
[If you do make that assumption, you can obtain estimates of and intervals for the relative shifts, just as you can with ANOVA. Well, it is also possible to obtain intervals without that assumption, but they're more difficult to interpret.]
If you look at the answer here, especially toward the end, it discusses the comparison between the t-test and the Wilcoxon-Mann-Whitney, which (when doing two-tailed tests at least) are the equivalent* of ANOVA and Kruskal-Wallis applied to a comparison of only two samples; it gives a little more detail, and much of that discussion carries over to the Kruskal-Wallis vs ANOVA.
* (aside a particular issue that arises with multigroup comparisons where you can have non-transitive pairwise differences)
It's not completely clear what you mean by a practical difference. You use them in generally a generally similar way. When both sets of assumptions apply they usually tend to give fairly similar sorts of results, but they can certainly give fairly different p-values in some situations.
Edit: Here's an example of the similarity of inference even at small samples -- here's the joint acceptance region for the location-shifts among three groups (the second and third each compared with the first) sampled from normal distributions (with small sample sizes) for a particular data set, at the 5% level:
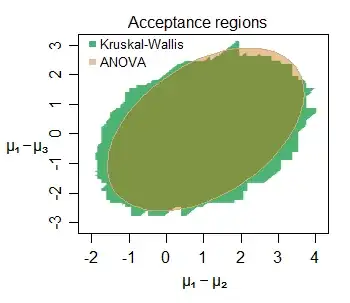
Numerous interesting features can be discerned -- the slightly larger acceptance region for the KW in this case, with its boundary consisting of vertical, horizontal and diagonal straight line segments (it is not hard to figure out why). The two regions tell us very similar things about the parameters of interest here.
Yes there is. The anova is a parametric approach while kruskal.test is a non parametric approach. So kruskal.test does not need any distributional assumption.
From practical point of view, when your data is skewed, then anova would not a be good approach to use. Have a look at this question for example.
As far as I know (but please correct me if I'm wrong cause I'm not sure), the Kruskal-Wallis test is constructed in order to detect a difference between two distributions having the same shape and the same dispersion, that is, one is obtained by translating the other by a difference $\Delta$, such as:
Let's call $(*)$ this assumption. The KW test tests the null hypothesis $H_0\colon\{\Delta=0\}$ vs $H_1\colon\{\Delta \neq 0\}$. However, the KW test is "valid" without assumption $(*)$ : its signficance level (probability to reject $H_0$ under $H_0)$ is valid because $(*)$ is obviously fulfilled under $H_0\colon\{\text{the distributions are equal}\}$.
But the KW test is "inefficient" if $(*)$ does not hold: it only intend to have a good power to detect $\Delta >0$, and then the test statistic is not appropriate to reflect the difference between the two distributions if there's no such $\Delta$.
Consider the following example. Two samples $x$ and $y$ of size $n=1000$ are generated from two quite different distributions but having the same mean. Then KW fails to reject $H_0$.
set.seed(666)
n <- 1000
x <- rnorm(n)
y <- (2*rbinom(n,1,1/2)-1)*rnorm(n,3)
plot(density(x, from=min(y), to=max(y)))
lines(density(y), col="blue")
> kruskal.test(list(x,y))
Kruskal-Wallis rank sum test
data: list(x, y)
Kruskal-Wallis chi-squared = 2.482, df = 1, p-value = 0.1152
As I claimed in the beginning, I'm not sure about the precise construction of KW. Maybe my answer is more correct for another nonparametric test (Mann-Whitney ?..), but the approach should be similar.
Kruskal-Wallis is rank based, rather than value-based. This can make a big difference if there are skewed distributions or if there are extreme cases
