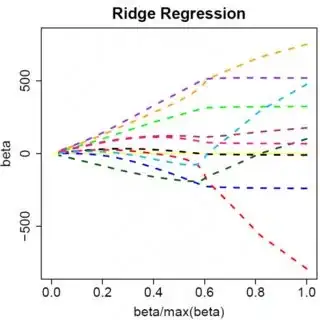
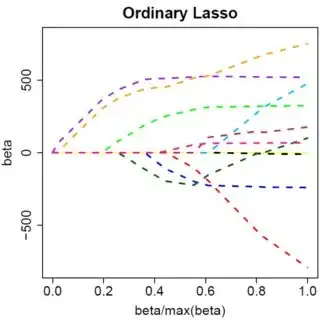
Let's consider a very simple model: $y = \beta x + e$, with an L1 penalty on $\hat{\beta}$ and a least-squares loss function on $\hat{e}$. We can expand the expression to be minimized as:
$\min y^Ty -2 y^Tx\hat{\beta} + \hat{\beta} x^Tx\hat{\beta} + 2\lambda|\hat{\beta}|$
Keep in mind this is a univariate example, with $\beta$ and $x$ being scalars, to show how LASSO can send a coefficient to zero. This can be generalized to the multivariate case.
Let us assume the least-squares solution is some $\hat{\beta} > 0$, which is equivalent to assuming that $y^Tx > 0$, and see what happens when we add the L1 penalty. With $\hat{\beta}>0$, $|\hat{\beta}| = \hat{\beta}$, so the penalty term is equal to $2\lambda\beta$. The derivative of the objective function w.r.t. $\hat{\beta}$ is:
$-2y^Tx +2x^Tx\hat{\beta} + 2\lambda$
which evidently has solution $\hat{\beta} = (y^Tx - \lambda)/(x^Tx)$.
Obviously by increasing $\lambda$ we can drive $\hat{\beta}$ to zero (at $\lambda = y^Tx$). However, once $\hat{\beta} = 0$, increasing $\lambda$ won't drive it negative, because, writing loosely, the instant $\hat{\beta}$ becomes negative, the derivative of the objective function changes to:
$-2y^Tx +2x^Tx\hat{\beta} - 2\lambda$
where the flip in the sign of $\lambda$ is due to the absolute value nature of the penalty term; when $\beta$ becomes negative, the penalty term becomes equal to $-2\lambda\beta$, and taking the derivative w.r.t. $\beta$ results in $-2\lambda$. This leads to the solution $\hat{\beta} = (y^Tx + \lambda)/(x^Tx)$, which is obviously inconsistent with $\hat{\beta} < 0$ (given that the least squares solution $> 0$, which implies $y^Tx > 0$, and $\lambda > 0$). There is an increase in the L1 penalty AND an increase in the squared error term (as we are moving farther from the least squares solution) when moving $\hat{\beta}$ from $0$ to $ < 0$, so we don't, we just stick at $\hat{\beta}=0$.
It should be intuitively clear the same logic applies, with appropriate sign changes, for a least squares solution with $\hat{\beta} < 0$.
With the least squares penalty $\lambda\hat{\beta}^2$, however, the derivative becomes:
$-2y^Tx +2x^Tx\hat{\beta} + 2\lambda\hat{\beta}$
which evidently has solution $\hat{\beta} = y^Tx/(x^Tx + \lambda)$. Obviously no increase in $\lambda$ will drive this all the way to zero. So the L2 penalty can't act as a variable selection tool without some mild ad-hockery such as "set the parameter estimate equal to zero if it is less than $\epsilon$".
Obviously things can change when you move to multivariate models, for example, moving one parameter estimate around might force another one to change sign, but the general principle is the same: the L2 penalty function can't get you all the way to zero, because, writing very heuristically, it in effect adds to the "denominator" of the expression for $\hat{\beta}$, but the L1 penalty function can, because it in effect adds to the "numerator".