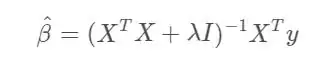4

I'm doing a little self study project, and am trying to implement OLS, Ridge, and Lasso regression from scratch using just Numpy, and am having problems getting this to work with Lasso regression.

To check my results I'm comparing my results with those returned by Scikit-Learn.

The coefficients for OLS can be derived from the following expression:

enter image description here

In numpy, this can be implemented in the following way:

np.linalg.inv(X.T @ X) @ (X.T @ y)

If I use the boston housing dataset from scikit learn with this equation my coefficients match what's returned from scikit learn exactly.

The coefficients from Ridge Regression can be represented with the following expression:

enter image description here

In numpy this can be represented in the following way:

np.linalg.inv(X.T @ X + alpha * np.identity(X.shape[1]) @ (X.T @ y)

Again, if I plug in the appropriate variables for X, y and alpha, my coefficients match what's output by Scikit Learn's Ridge class.

However, I run into large discrepancies when I try to match the results from its Lasso.

I believe the coefficients for Lasso Regression can be derived in the following way:

enter image description here

I haven't seen this coded anywhere on the web, but I assume its implementation would look like this:

np.linalg.inv(X.T @ X) @ (X.T @ y - alpha*np.ones(X.shape[1]))

This returns results, but they do not match what's in scikit learn, and it's not particularly close. If I run a Lasso regression with alpha set to 10 in scikit learn on the boston dataset half of the coefficients are shrunk to zero. Whereas with my implementation they are shrunk only slightly.

What mistake am I making in getting Lasso to work?

Thank you.

Jonathan Bechtel
  • 287
  • 1
  • 8
  • See here: https://en.wikipedia.org/wiki/Lasso_(statistics)#Correlated_covariates – Demetri Pananos Mar 24 '19 at 03:18
  • @DemetriPananos - ie, I'm not getting the same results because Lasso itself requires a level of independence between my variables that I don't have, so the two methods are returning different values? – Jonathan Bechtel Mar 24 '19 at 03:20
  • Though I am not confident in the implementation of Lasso in sklearn, it could be the case that sklearn's optimizer is converging to a different a different, yet equivalent optima. I'm about to go grab Hastie's book and see if he writes anything about this. – Demetri Pananos Mar 24 '19 at 03:24
  • If you look through the documentation, the class for Lasso regression is inherited from the Elastic Net, so I believe they are implementing it as a special case of that, so maybe if I tried to do it that way I'd get better results. – Jonathan Bechtel Mar 24 '19 at 03:26
  • Looks like the source code says they use coordinate descent. It is likely coordinate descent converges to a different optima. – Demetri Pananos Mar 24 '19 at 03:29
  • 2
    Where does the formula you quote for the lasso solution come from? I don't believe there is a closed form solution for the lasso coefficients. – Matthew Drury Mar 24 '19 at 04:26
  • @MatthewDrury I inferred it from the answer given here: https://stats.stackexchange.com/questions/74542/why-does-the-lasso-provide-variable-selection – Jonathan Bechtel Mar 24 '19 at 20:26
  • 2
    Ahhh. That makes sense now. Unfortunately, the formulas in that answer do not generalize to the multi feature case. I'll write up an answer this evening that explains in more detail. – Matthew Drury Mar 24 '19 at 22:29
  • Lasso does not have closed form solution. Therefore, it is very normal to encounter such discrepancy. – verdery Feb 02 '20 at 23:56

1 Answers1

2

As @verdery and @Matthew Drury wrote in the comment above, there is no analytical expression for Lasso Regression like there is for Ordinary Least Square and Ridge Regression. Anyway, I tested your Ridge Regression $\hat{\beta}$ code

np.linalg.inv(X.T @ X + alpha * np.identity(X.shape[1]) @ (X.T @ y)

I used an X-matrix of shape (1600,12). What happened is that $\hat{\beta}$ (which is supposed to be a (12,1) shaped array/vector) became a (12,12) shaped matrix. Then I did a change in the code and wrote it like this instead:

np.linalg.inv(X.T.dot(X) + alpha * np.identity(X.shape[1])).dot(X.T).dot(y)

Now I got the right (12,1) shape of my $\hat{\beta}$ vector

bjornsing
  • 159
  • 10