Update: 7 Apr 2011
This answer is getting quite long and covers multiple aspects of the problem at hand. However, I've resisted, so far, breaking it into separate answers.
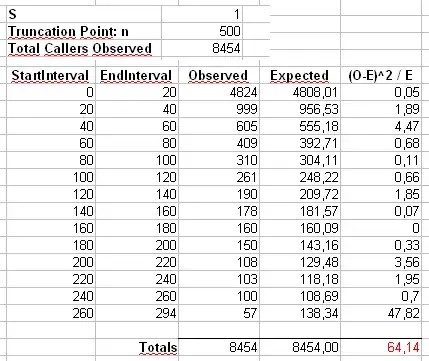
I've added at the very bottom a discussion of the performance of Pearson's $\chi^2$ for this example.
Bruce M. Hill authored, perhaps, the "seminal" paper on estimation in a Zipf-like context. He wrote several papers in the mid-1970's on the topic. However, the "Hill estimator" (as it's now called) essentially relies on the maximal order statistics of the sample and so, depending on the type of truncation present, that could get you in some trouble.
The main paper is:
B. M. Hill, A simple general approach to inference about the tail of a distribution, Ann. Stat., 1975.
If your data truly are initially Zipf and are then truncated, then a nice correspondence between the degree distribution and the Zipf plot can be harnessed to your advantage.
Specifically, the degree distribution is simply the empirical distribution of the number of times that each integer response is seen,
$$
d_i = \frac{\#\{j: X_j = i\}}{n} .
$$
If we plot this against $i$ on a log-log plot, we'll get a linear trend with a slope corresponding to the scaling coefficient.
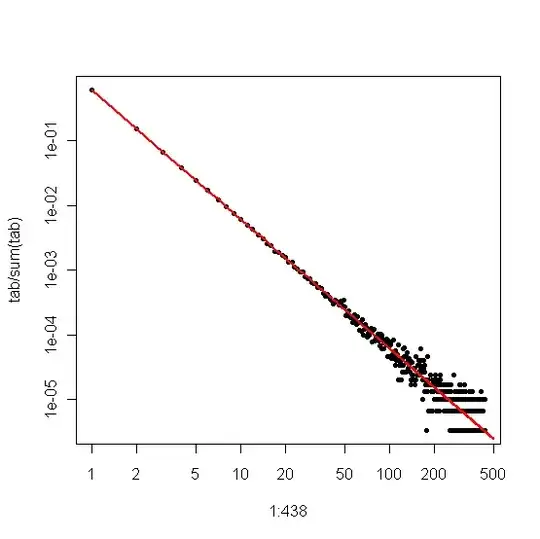
On the other hand, if we plot the Zipf plot, where we sort the sample from largest to smallest and then plot the values against their ranks, we get a different linear trend with a different slope. However the slopes are related.
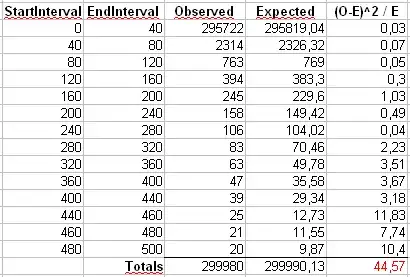
If $\alpha$ is the scaling-law coefficient for the Zipf distribution, then the slope in the first plot is $-\alpha$ and the slope in the second plot is $-1/(\alpha-1)$. Below is an example plot for $\alpha = 2$ and $n = 10^6$. The left-hand pane is the degree distribution and the slope of the red line is $-2$. The right-hand side is the Zipf plot, with the superimposed red line having a slope of $-1/(2-1) = -1$.
So, if your data have been truncated so that you see no values larger than some threshold $\tau$, but the data are otherwise Zipf-distributed and $\tau$ is reasonably large, then you can estimate $\alpha$ from the degree distribution. A very simple approach is to fit a line to the log-log plot and use the corresponding coefficient.
If your data are truncated so that you don't see small values (e.g., the way much filtering is done for large web data sets), then you can use the Zipf plot to estimate the slope on a log-log scale and then "back out" the scaling exponent. Say your estimate of the slope from the Zipf plot is $\hat{\beta}$. Then, one simple estimate of the scaling-law coefficient is
$$
\hat{\alpha} = 1 - \frac{1}{\hat{\beta}} .
$$
@csgillespie gave one recent paper co-authored by Mark Newman at Michigan regarding this topic. He seems to publish a lot of similar articles on this. Below is another along with a couple other references that might be of interest. Newman sometimes doesn't do the most sensible thing statistically, so be cautious.
MEJ Newman, Power laws, Pareto distributions and Zipf's law, Contemporary Physics 46, 2005, pp. 323-351.
M. Mitzenmacher, A Brief History of Generative Models for Power Law and Lognormal Distributions, Internet Math., vol. 1, no. 2, 2003, pp. 226-251.
K. Knight, A simple modification of the Hill estimator with applications to robustness and bias reduction, 2010.
Addendum:
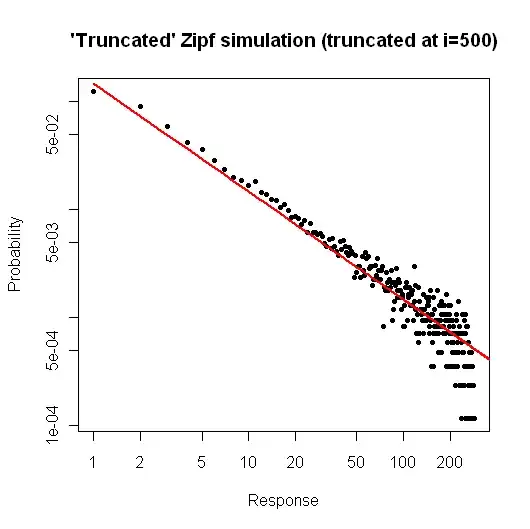
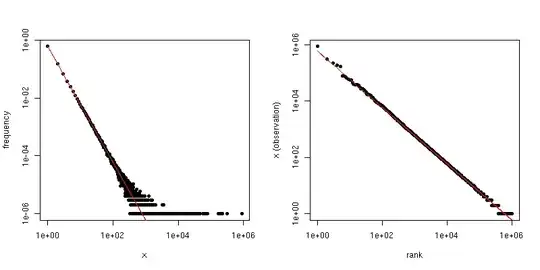
Here is a simple simulation in $R$ to demonstrate what you might expect if you took a sample of size $10^5$ from your distribution (as described in your comment below your original question).
> x <- (1:500)^(-0.9)
> p <- x / sum(x)
> y <- sample(length(p), size=100000, repl=TRUE, prob=p)
> tab <- table(y)
> plot( 1:500, tab/sum(tab), log="xy", pch=20,
main="'Truncated' Zipf simulation (truncated at i=500)",
xlab="Response", ylab="Probability" )
> lines(p, col="red", lwd=2)
The resulting plot is
From the plot, we can see that the relative error of the degree distribution for $i \leq 30$ (or so) is very good. You could do a formal chi-square test, but this does not strictly tell you that the data follow the prespecified distribution. It only tells you that you have no evidence to conclude that they don't.
Still, from a practical standpoint, such a plot should be relatively compelling.
Addendum 2: Let's consider the example that Maurizio uses in his comments below. We'll assume that $\alpha = 2$ and $n = 300\,000$, with a truncated Zipf distribution having maximum value $x_{\mathrm{max}} = 500$.
We'll calculate Pearson's $\chi^2$ statistic in two ways. The standard way is via the statistic
$$
X^2 = \sum_{i=1}^{500} \frac{(O_i - E_i)^2}{E_i}
$$
where $O_i$ is the observed counts of the value $i$ in the sample and $E_i = n p_i = n i^{-\alpha} / \sum_{j=1}^{500} j^{-\alpha}$.
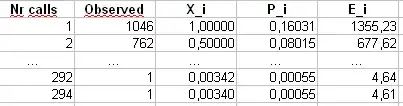
We'll also calculate a second statistic formed by first binning the counts in bins of size 40, as shown in Maurizio's spreadsheet (the last bin only contains the sum of twenty separate outcome values.
Let's draw 5000 separate samples of size $n$ from this distribution and calculate the $p$-values using these two different statistics.
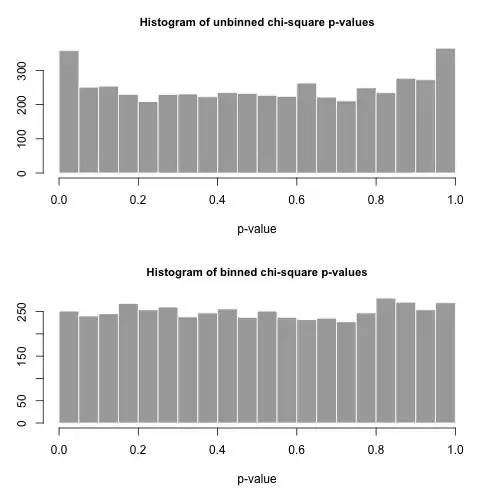
The histograms of the $p$-values are below and are seen to be quite uniform. The empirical Type I error rates are 0.0716 (standard, unbinned method) and 0.0502 (binned method), respectively and neither are statistically significantly different from the target 0.05 value for the sample size of 5000 that we've chosen.
Here is the $R$ code.
# Chi-square testing of the truncated Zipf.
a <- 2
n <- 300000
xmax <- 500
nreps <- 5000
zipf.chisq.test <- function(n, a=0.9, xmax=500, bin.size = 40)
{
# Make the probability vector
x <- (1:xmax)^(-a)
p <- x / sum(x)
# Do the sampling
y <- sample(length(p), size=n, repl=TRUE, prob=p)
# Use tabulate, NOT table!
tab <- tabulate(y,xmax)
# unbinned chi-square stat and p-value
discrepancy <- (tab-n*p)^2/(n*p)
chi.stat <- sum(discrepancy)
p.val <- pchisq(chi.stat, df=xmax-1, lower.tail = FALSE)
# binned chi-square stat and p-value
bins <- seq(bin.size,xmax,by=bin.size)
if( bins[length(bins)] != xmax )
bins <- c(bins, xmax)
tab.bin <- cumsum(tab)[bins]
tab.bin <- c(tab.bin[1], diff(tab.bin))
prob.bin <- cumsum(p)[bins]
prob.bin <- c(prob.bin[1], diff(prob.bin))
disc.bin <- (tab.bin - n*prob.bin)^2/(n * prob.bin)
chi.stat.bin <- sum(disc.bin)
p.val.bin <- pchisq(chi.stat.bin, df=length(tab.bin)-1, lower.tail = FALSE)
# Return the binned and unbineed p-values
c(p.val, p.val.bin, chi.stat, chi.stat.bin)
}
set.seed( .Random.seed[2] )
all <- replicate(nreps, zipf.chisq.test(n, a, xmax))
par(mfrow=c(2,1))
hist( all[1,], breaks=20, col="darkgrey", border="white",
main="Histogram of unbinned chi-square p-values", xlab="p-value")
hist( all[2,], breaks=20, col="darkgrey", border="white",
main="Histogram of binned chi-square p-values", xlab="p-value" )
type.one.error <- rowMeans( all[1:2,] < 0.05 )