Hierarchical Bayes Normal-Normal Model

Question

I have the following data for 8 runners in a 100 meter dash:

runner 1 88 91 87 82
runner 2 81 85 78 91
runner 3 75 77 83 81
runner 4 92 89 84 82
runner 5 78 79 84 92
runner 6 89 75 79 83
runner 7 91 89 92 91
runner 8 87 86 88 91

The ratings represent a performance rating and are normally distributed with unknown mean and unknown variance. Each runner can be considered as a sub-group with a mean and variance.

Any guidance will be highly appreciated

Answer 1

My example here may help: When making inferences about group means, are credible Intervals sensitive to within-subject variance while confidence intervals are not?

I modified the model slightly for your data. Note that with such little data your results will be heavily dependent on the priors you use so I would attempt modifying the priors on the group means and precisions (1/variance) and seeing the different results to learn.

Here are the results I got:

This is modified from John Krushke's example here: http://psy2.ucsd.edu/~dhuber/cr_SimpleLinearRegressionRepeatedBrugs.R

He has a helpful website and blog: http://www.indiana.edu/~kruschke/DoingBayesianDataAnalysis/

#Note. To use rjags you need to first install JAGS from here: 
#http://sourceforge.net/projects/mcmc-jags/files/

install.packages("rjags") #run first time to install package

require(rjags) #load rjags package


#Format your data
subID<-rep(1:8,each=4)

dat<-rbind(88, 91, 87, 82,
81, 85, 78, 91,
75, 77, 83, 81,
92, 89, 84, 82,
78, 79, 84, 92,
89, 75, 79, 83,
91, 89, 92, 91,
87, 86, 88, 91
)

dat<-cbind(subID,dat)
colnames(dat)<-c("Subject","Value")
dat<-as.data.frame(dat)



#Jags fit function
jags.fit<-function(dat){

  #Create JAGS model
  modelstring = "

  model{
  for(n in 1:Ndata){
  y[n]~dnorm(mu[subj[n]],tau[subj[n]]) T(0, )
  }

  for(s in 1:Nsubj){
  mu[s]~dnorm(muG,tauG) T(0, )
  tau[s] ~ dgamma(5,5)
  }


  muG~dnorm(80,.01) T(0, )
  tauG~dgamma(1,1)

  }
  "
  writeLines(modelstring,con="model.txt")

#############  

  #Format Data
  Ndata = nrow(dat)
  subj = as.integer( factor( dat$Subject ,
                                 levels=unique(dat$Subject ) ) )
  Nsubj = length(unique(subj))
  y = as.numeric(dat$Value)

  dataList = list(
    Ndata = Ndata ,
    Nsubj = Nsubj ,
    subj = subj ,
    y = y
  )

  #Nodes to monitor
  parameters=c("muG","tauG","mu","tau")


  #MCMC Settings
  adaptSteps = 1000             
  burnInSteps = 1000            
  nChains = 1                   
  numSavedSteps= nChains*10000          
  thinSteps=20                      
  nPerChain = ceiling( ( numSavedSteps * thinSteps ) / nChains )            


  #Create Model
  jagsModel = jags.model( "model.txt" , data=dataList, 
                          n.chains=nChains , n.adapt=adaptSteps , quiet=FALSE )
  # Burn-in:
  cat( "Burning in the MCMC chain...\n" )
  update( jagsModel , n.iter=burnInSteps )

  # Getting DIC data:
  load.module("dic")


  # The saved MCMC chain:
  cat( "Sampling final MCMC chain...\n" )
  codaSamples = coda.samples( jagsModel , variable.names=parameters , 
                              n.iter=nPerChain , thin=thinSteps )  

  mcmcChain = as.matrix( codaSamples )

  result = list(codaSamples=codaSamples, mcmcChain=mcmcChain)

}


output<-jags.fit(dat) # fit the model to your data



###make plots
##Overall plots
par(mfrow=c(2,1))
#Plot overall means
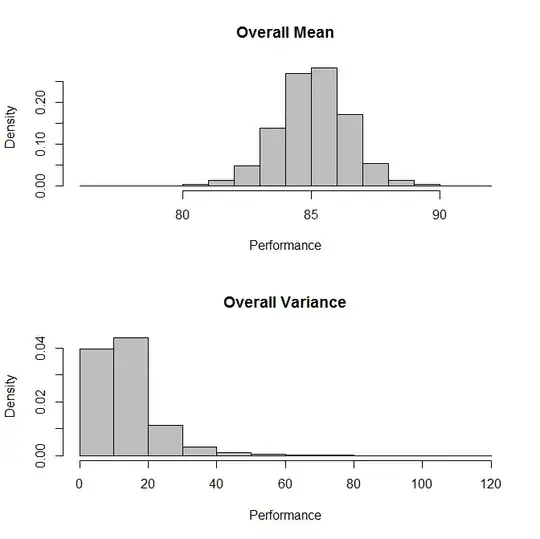
hist(output$mcmcChain[,"muG"],col="Grey", freq=F,
main="Overall Mean", xlab="Performance"
)
#Plot overall variance
hist(1/output$mcmcChain[,"tauG"],col="Grey", freq=F,
main="Overall Variance", xlab="Performance")


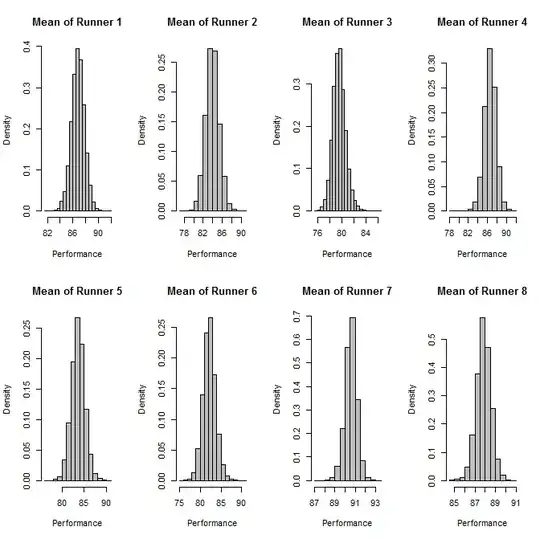
##Indidvidual Mean Plots
dev.new()
par(mfrow=c(2,4))
for(i in 1:8){
hist(output$mcmcChain[,paste("mu[",i,"]",sep="")],
main=paste("Mean of Runner", i), xlab="Performance", freq=F, col="Grey"
)
}


##Indidvidual Variance Plots
dev.new()
par(mfrow=c(2,4))
for(i in 1:8){
hist(1/output$mcmcChain[,paste("tau[",i,"]",sep="")],
main=paste("Variance of Runner", i), xlab="Performance", freq=F, col="Grey"
)
}

# see what is in the output
attributes(output$mcmcChain)

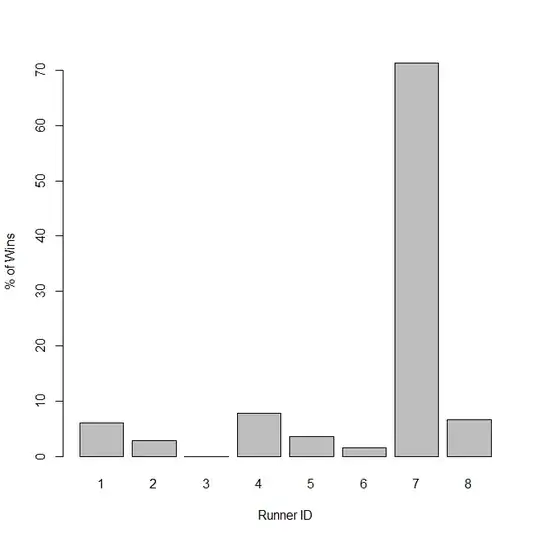
Edit: To see the percent of time the model predicts each runner will win we can take the mean and variance estimated for each individual at each mcmc step, then sample a performance from a distribution determined by those parameters. We can then simply count the number of times each runner had the highest performance.

nSamps<-length(output$mcmcChain[,paste("mu[",i,"]",sep="")])
out=matrix(nrow=nSamps*8,ncol=3)
cnt<-1
for(j in 1:nSamps){
for(i in 1:8){
m<-output$mcmcChain[,paste("mu[",i,"]",sep="")][j]
v<-1/output$mcmcChain[,paste("tau[",i,"]",sep="")][j]
t<-rnorm(1,m,sqrt(v))
out[cnt,]<-cbind(j,i,t)
cnt<-cnt+1
}
}
colnames(out)<-c("N","RunnerID","Time")


winners=matrix(nrow=nSamps,ncol=1)
for(i in 1:nSamps){
sub<-out[which(out[,"N"]==i),]
winners[i]<-sub[which(sub[,"Time"]==max(sub[,"Time"])),"RunnerID"]
}

dev.new()
barplot(100*table(winners)/nSamps, xlab="Runner ID", ylab="% of Wins")