Let a discrete Random Variable $T$ have CDF $F_T(T)$. Could you please help me understand why $$ P \left[ F_T (T) \leq a_1 \right] \leq a_1 $$
I know that the result holds with equality for the continuous case, it is known as Probability Integral Transform, but I am having trouble understanding it for the Discrete one since the inverse is not defined. Thank you.
Consider a box $\Omega$ filled with tickets. On each ticket $\omega$ is written a number called $X(\omega)$. For any number $x$, whether or not it appears among the tickets, $F_X(x)$ is (defined to be) the proportion of tickets for which $X \le x.$
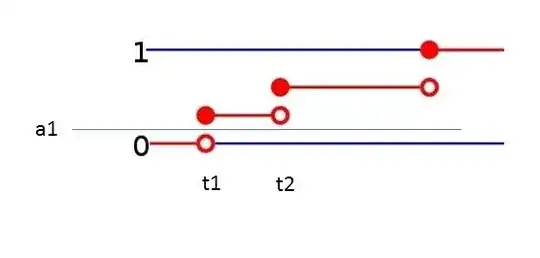
Let's add some new information to each ticket $\omega$: next to the value of $X$ written on it, we will also write the value of $F_X(X(\omega))$: it is the proportion of all tickets with values of $X$ less than or equal to this value, $X(\omega).$ (It's the same concept as a percentile or quantile: the tickets with the smallest values of $X$ get the smallest proportions and the tickets with the largest values of $X$ get the largest proportions.) These new values, being proportions, lie between $0$ and $1$ inclusive. But, when $X$ is discrete, they will not include all possible numbers, but only the proportions that actually occur in the box.
Consider drawing a single ticket from this box at random. Fixing a number $a$ in advance, what is the chance that the new value (the "quantile") written on the ticket will not exceed $a$? Of course it's the proportion of tickets with values of $a$ or lower. But all such tickets, by construction, have values of $X$ that lie within the lower $100a\%$ of all the values. Therefore this chance cannot exceed $a$.
The chance might be strictly less than $a$ when $a$ is not one of the actual proportions in the box. Because it cannot be greater than $a$ and now cannot be equal to $a$ it has to be less than $a$!
A simple example is afforded by a box with two tickets: on one of these $X$ equals $0$ and on the other it equals $1$. When we write the proportions on the tickets, then, we will write $1/2$ (or $50\%$) on the first ticket (because half the tickets have values of $0$ or less) and $1$ (or $100\%$) on the second ticket (because all the tickets have values of $1$ or less).
What is the chance that this new value on a randomly drawn ticket will be less than or equal to $a=3/4$ (or $75\%$)? Because the new values are only $50\%$ and $100\%$, and half of them are less than $75\%$, the answer obviously is $1/2$. This is strictly less than $a$ because there are no proportions in the box between $50\%$ and $75\%$. The issue is just that trivial and simple.
The preceding used a tickets in a box metaphor for reasoning about random variables. If we replace $\Omega$ by a probability space, insist that $X$ be a measurable function, and understand "proportion" as the value of the probability measure, then we will have a rigorous proof. And it's still just as trivial.
Try to draw CDF of a Discrete random variable like the (upper) one you have here. Now draw a horizontal line to indicate the level of $a_1$. All you need to do is to find the values of $T$ such that your CDF i.e. $F_T$ satisfies $F_T(T)\leq a_1$. You can move your $a_1$ vertically. Now depending on the level of $a_1$ sometimes you get $P[F_T(T)\leq a_1]<a_1$ and sometimes $P[F_T(T)\leq a_1]= a_1$. The equality happens when your $a_1$ is equal to one of those horizontal (red) lines in the plot of your CDF. OK, see $a_1$ in the graph below. 
For what values of $T$ you have $F_T(T)\leq a_1$? Obviously for $t<t_1$. For $t<t_1$, $P_T(t)=P(T< t_1)=0$. And as the plot shows you have $0<a_1$. So the condition you want to prove is correct in this case. Now look at $a_1$ below. 
Again for what values of $T$ you have $F_T(T)\leq a_1$? Obviously for all $t< t_2$. Now if $t_1\leq t< t_2$ we have $P_T(t)=P(T\leq t)=a_1$. In this case you will end up with equality i.e. $P[F_T(T)\leq a_1]= a_1$. And if $t<t_1$ then $P_T(t)=P(T\leq t)=0$. Here again as the graph shows the condition holds i.e. $0\leq a_1$. You can do exactly the same argument if you move $a_1$ vertically.
