The question establishes a context suggesting that a distribution free tolerance interval is needed. This means
A specific shape for the distribution will not be assumed.
The endpoints of the interval will be estimated from the data.
The interval is intended to enclose a given amount of the distribution, such as its middle 68%. When it is understood that this amount will apply to the middle of the distribution, the tolerance interval is said to be symmetric and two-sided and the amount $\gamma = 68\%$ is called its coverage.
Because the interval is based on a random sample, it is random. It is desired to control the chance that it fails to attain at least the required coverage. Let this chance be limited to a value $\alpha$. (Often $\alpha$ is chosen to be around $0.05 = 5\%$.) The value $1-\alpha$ is called the confidence of the interval.
The solution is to modify an online quantile estimation procedure in order to keep a running account of the order statistics needed to bound the tolerance interval. This answer explains these terms, derives the needed formulas (which are remarkably simple, requiring only the ability to compute Binomial quantiles), gives references to the relevant algorithms, and provides working code to compute nonparametric tolerance intervals.
The standard reference--which can serve both as a textbook and a handbook--is
Gerald J. Hahn and William Q. Meeker, Statistical Intervals. A Guide for Practitioners. John Wiley & Sons, 1991.
(Bill Meeker told me recently that a new edition is coming out soon.)
As in many nonparametric procedures, such intervals are based on the order statistics. These are the values of the sorted data, which we may suppose are a realization of random variables
$$X_1 \le X_2 \le \cdots \le X_n.$$
The interval will be bounded by two of these order statistics, $X_l \le X_u$. To determine which indexes should be used for $l$ and $u$, use the defining criteria:
Symmetry: $l+u$ should be as near to $n+1$ as possible.
Coverage and confidence: the chance that the interval $[X_l, X_u]$ fails to cover at least $\gamma$ of the underlying distribution $F$ should be at most $\alpha$.
We have to compute this chance of failure, which is
$${\Pr}_F(F(X_u) - F(X_l) \lt \gamma).$$
If we only assume $F$ is continuous (which means ties are impossible), applying the probability integral transform shows that
$${\Pr}_F(F(X_u) - F(X_l) \lt \gamma) = \Pr(Y_u - Y_l \lt \gamma)$$
for order statistics $Y_u$ and $Y_l$ obtained from $n$ independent uniformly distributed variables (on the interval $[0,1]$). Their joint density is
$$f_{l,u}(y_l, y_u) = \binom{n}{l-1, 1, u-l-1, 1, n-u} (y_l)^{l-1}(y_u-y_l)^{u-l-1}(1-y_u)^{n-u},$$
defined for all $0 \le y_l \le y_u \le 1$. The multinomial coefficient can be computed as
$$\binom{n}{l-1, 1, u-l-1, 1, n-u} = \frac{n!}{(l-1)!(u-l-1)!(n-u)!}.$$
Recognizing $y_u-y_l$ as the quantity we want to work with, change variables to $y_u-y_l = z$, so that $y_u = y_l + z$. The Jacobian of this transformation has unit determinant, so all we need to do is substitute and integrate out $y_l$:
$$f_{l,u}(z) = z^{u-l-1}\frac{n!}{(l-1)!(u-l-1)!(n-u)!}\int_0^{1-z} (y_l)^{l-1}(1-y_l-z)^{n-u}dy_l$$
The substitution $y_l = (1-z)x$ does the trick, giving
$$f_{l,u}(z) = \frac{n!}{(l+n-u)!(u-l-1)!}z^{u-l-1}(1-z)^{l+n-u}.$$
It is a Beta$(u-l, l+n-u+1)$ distribution. Equivalently, the chance that $Z \lt \gamma$ is given by the upper tail of the associated Binomial distribution:
$$\Pr(Z \lt \gamma) = \sum_{j=u-l}^n \binom{n}{j}\gamma^j(1-\gamma)^{n-j}.$$
The solution is
Select $u$ and $l$ so that (1) $u+l$ is close to $n$ and (2) $u+l-1$ equals or exceeds the $1-\alpha$ quantile of a Binomial$(\gamma, n)$ distribution. The tolerance interval is bounded by the order statistics $X_l$ and $X_u$.
This is the formula (5.2) given by Hahn & Meeker (without any derivation).
BTW, when $F$ is not continuous, then the coverage may be greater than intended, but it should not be any less. Equivalently, the confidence is greater than intended.
For example, with $\gamma=68\%$, $\alpha=5\%$, and a sample of $n=100$, this formula gives $l=12, u=89$. The $95\%$ confidence, $68\%$ coverage symmetric nonparametric tolerance interval is $[X_{12}, X_{89}]$. The reason this includes $89-12+1 = 78 = 78\%$ of the data, rather than just $68\%$, is the need to be $95\%$ confident that the coverage of $68\%$ really is attained.
The discrepancy between the proportion of data that are included in this interval and the proportion of the distribution that must be covered will become vanishingly small as the sample size increases. Thus, once the sample size is sufficiently large, $X_l$ and $X_u$ are approximating the $(1-\gamma)/2$ and $(1+\gamma)/2$ quantiles of the distribution. Consequently, an online calculation of this tolerance interval can be performed by means of a pair of online quantile calculations..
Working R code to compute $l$ and $u$, together with a simulation to study the actual distribution of coverages, is given below. Here is an example of its output for a sample of size $n=100$ using $l=12, u=89$ in order to achieve $68\%$ coverage with $95\%$ confidence.
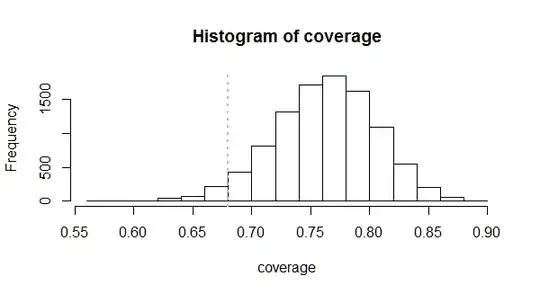
It shows that this method works because very close to $95\%$ of the coverages in these $10,000$ samples actually equalled or exceeded $68\%$. They averaged around $76\%$ and sometimes got as large as $89\%$. When they failed, they did not fail too badly, almost always covering at least $60\%$ of the distribution.
#
# Nonparametric tolerance interval simulation
# See Hahn & Meeker Table A.16 and section 5.3.1.
#
gamma <- 0.68 # Coverage
alpha <- 0.05 # Size
n <- 100 # Sample size
u.m.l <- ceiling(qbinom(1-alpha, n, gamma)) + 1
u.p.l <- n + ifelse((n - u.m.l) %% 2 == 1, 1, 0)
u <- (u.p.l + u.m.l)/2
l <- (u.p.l - u.m.l)/2
(l + n - u + 1) # Number removed from ends (Hahn & Meeker)
(pbeta(gamma, u-l, l+n-u+1)) # Should be barely less than alpha
set.seed(17)
n.sim <- 1e4
x.sim <- apply(matrix(runif(n.sim*n), nrow=n), 2, sort)
coverage <- x.sim[u, ] - x.sim[l, ]
hist(coverage)
abline(v=gamma, lty=3, lwd=2, col="Gray")
mean(coverage >= gamma)
