3

I observe a series of crime incidents linked by modus operandi or some other peculiar characteristic of the crime (e.g. cutting catalytic converters from underneath vehicles). I would like to know if the observed days of the week that the crimes occur on (ignoring the uncertainty that sometimes occur in crime incidents - e.g. it happens overnight) are random. I typically have very few linked crime events, say between 5-15.

So question 1, there is a lot of knowledge about using Pearson's $\chi^2$ on small n contingency tables, can I use all of that same advice for $2\times 2$ contingency tables that come with it for just 7 day of week bins? (In particular can I use the $N - 1$ correction given expected cell frequencies are at least 1 and still expect similar coverage rates - which would mean I need at least 7 observed events?)

Or alternatively question 2, are there any other obvious approaches I can take to test the hypothesis of the events being random with respect to the day of the week? (Permutation approaches perhaps given the limited nature of the potential permutations?)

Community
  • 1
Andy W
  • 15,245
  • 8
  • 69
  • 191
  • I presume ignoring the cyclical nature of days of week simplifies the problem - if not and it potentially increases the power of whatever test I would love to hear about that solution as well. – Andy W Oct 25 '13 at 13:39
  • If I get you correctly, you have variable "week" with categories Mon through Sun, and you are testing the hypothesis that the probability distribution is even (which corresponds to complete randomness). If so, there are two options coming to my mind... – ttnphns Oct 25 '13 at 14:10
  • (cont.) (1) You treat "week" as nominal. Then H0 is about even multinomial distribution; use one-sample Chi-square test. (2) You treat "week" as (discretized) continuous. Then H0 is about uniform distribution. K-S test comes to mind, but because "week" is circular, not linear variable, the circular analogue of the test, [Kuiper's test](http://www.answers.com/topic/kuiper-s-test) should be used. In the situation of low frequences, exact or Monte Carlo versions of the tests should be preferred. – ttnphns Oct 25 '13 at 14:10
  • Thank you @ttnphns (you understand correctly). For the Pearson Chi-Square test what should I use as the degrees of freedom (5 or 6)? For some reason I thought the K-S was inappropriate for small samples, but I see that is not the case. – Andy W Oct 25 '13 at 14:32
  • As I know, one-sample Chi-sq test has df= num._of_categories-1. But in exact regime (which I believe you'll choose) you don't need any df. As for Kuiper, I just don't know if the exact procedure has been implemented. – ttnphns Oct 25 '13 at 14:44
  • I was hoping the N-1 correction suggested for 2x2 contingency tables would also apply here (which would mean 5 degrees of freedom). Wishful thinking perhaps, but it lends itself to smaller expected cell frequencies. I'm unfamiliar with the exact tests - do I generate all permutations and then assign them probabilities given the null model? – Andy W Oct 25 '13 at 15:18
  • 2
    This does not appear to be a contingency table setting, but rather a test of a uniform distribution. The usual $\chi^2$ test, using the permutation distribution of the null to compute the p-value, will be one of your best bets and actually has some appreciable power to detect variation with such small datasets. (An adequate answer to support this opinion would require an extensive simulation study, which I have only partially carried out.) – whuber Oct 25 '13 at 15:42
  • @Andy, no. As I've said (and whuber corroborated it) this is one-sample testing of evenness of a frequency distribution. It isn't 2-sample test (a contingency-table test). I recommend you to try Kuiper or something similar. – ttnphns Oct 25 '13 at 16:32
  • Thanks @whuber, Any advice about how to go about generating the permutations (and how to assign them the area of the null) I would appreciate. – Andy W Oct 25 '13 at 16:34
  • Andy, ftp://public.dhe.ibm.com/software/analytics/spss/documentation/statistics/20.0/en/client/Manuals/IBM_SPSS_Exact_Tests.pdf decribes exact testing for 1-sample Chi-sq and K-S tests in SPSS, see from page 39. I suppose (but not sure) that the same logic would be applied to Kuiper test. – ttnphns Oct 25 '13 at 17:16
  • @whuber and ttnphns, I have posted an answer and would appreciate if you would have a look to see if I have gone awry in anyplace. – Andy W Nov 05 '13 at 15:03

1 Answers1

1

I will walk through how I generated the exact statistics for the $\chi^2$ distribution and (hopefully) update later with a paper that gives tables for the exact distributions and where the exact distribution converges to the theoretical $\chi^2$ with $6$ degrees of freedom. Ditto for the K-S and Kuiper distributions that ttnphns mentions.

So the steps to generate the exact distributions are:

  1. Generate all potential combinations of outcomes allocating crimes into the $7$ weekday bins. The total number of combinations ends up being $\binom{M + N - 1}{M - 1}$ where $M = 7$ weekday bins and $N$ equals the number of crimes observed.
  2. For each of the combinations, calculate the probability of observing that outcome under the null hypothesis. Here the null is that each crime has a multinomial distribution in which the weekdays are the outcomes and are equi-probable (e.g. each day has a probability of $1/7$ of being selected).
  3. Generate the test statistic for that set of observations.

From this information you can generate critical values for the test distributions under the null. So If you observe $3$ crimes, with two occurring on Monday and one on Tuesday, the probability of that event under the null is:

$$Pr(\text{Mon.} = 2, \text{Tues.} = 1) = \frac{3!}{2!1!} \cdot ({P_m}^2)({P_t}^1) = 0.00874635568513119$$

Where $P_m$ and $P_t$ symbolize the probability of an event on Monday and Tuesday respectively, and $P_m = P_t = 1/7$. (If you wanted to generalize to a window in which say spans 10 days, you may want to consider unequal probalities of $2/10$ for the overlapping days and $1/10$ for the others.)

For an example of generating the exact distribution of the test statistic, with three crimes there are only three different possible $\chi^2$ values out of the 84 different combinations (since order doesn't matter for the statistic). The below table symbolizes these potential outcomes. (Just imagine sorting the days of the week so the day of the week with the most events is in the left most column.)

A  B   C
.
.  .
.  ..  ...

Subsequently, combinations of A appear 7 times, B 42 times, and C 35 times. The below table shows the probabilties of obtaining said $\chi^2$ statistics and how to generate the CDF of the null hypothesis. From here you can see that it is actually possible to reject the null at a .05 critical level if all three events are observed on the same day.

    #  ChiSq    Prob(Sum) CDF
C  35    4         .61    .61
B  42    8.67      .37    .98
A   7   18         .02   1.0

Also from the set of all potential combinations you can generate the distributions under various alternative hypotheses, and this allows you to evaluate the power of the test under those circumstances. So for example for $5$ crimes, the exact $\chi^2$ distribution has a $.05$ critical value at $10.4$. So for an alternative hypothesis of data having positive probability in only two days, you have 100% power (i.e. the only observable $\chi^2$ values if 5 crimes occur in 2 or fewer days of the week is over $10.4$).

The image below shows the CDFs for the exact $\chi^2$ distribution with $5$ crimes in $7$ weekday bins (in light grey lines), CDFs for different alternative hypotheses in dark grey lines, and the critical value $\chi^2$ highlighted with a red guideline. The alternative hypotheses are for differing numbers of days that are equi-probable for the crimes to occur on for $1$ to $4$ days during the week.

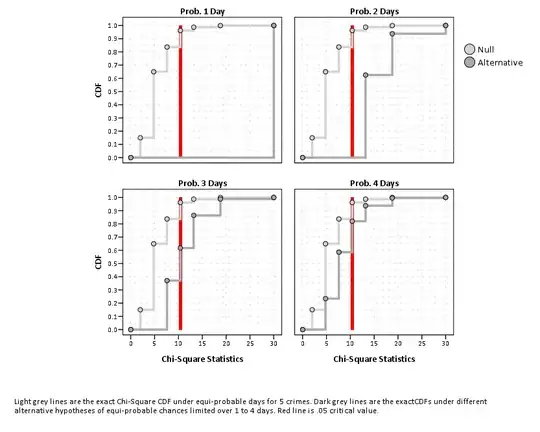
enter image description here

You can see from this chart even for an alternative of equi-probable chances over three days for just 5 crimes the power is just under 40%, 1 minus the CDF of the alt. hypothesis where it intersects the critical value. (Earlier I wrote that a tie goes to rejecting the null, but that would be incorrect as the Type 1 error would be inflated to .39 instead of .02 in my 3 crimes example.)

I have a paper going through this same analysis and generating critical values for Kuiper's $V$ and the $\chi^2$ test now posted on SSRN, Testing for Randomness in Day of Week Crime Sprees with Small Samples.

Andy W
  • 15,245
  • 8
  • 69
  • 191