I have a data frame with the following:
> summary(d5$points)
Min. 1st Qu. Median Mean 3rd Qu. Max.
-4.200 0.000 1.000 2.579 5.000 23.400
> sd(d5$points)
[1] 3.736616
What's a simple, but statistically sound way to categorize this data into terrible, poor, average, good, excellent.
I'm using R.
Edit:
Higher is points is better. Negative points is terrible. A good game would be a player scoring 6+ points, but that's just from my observations.
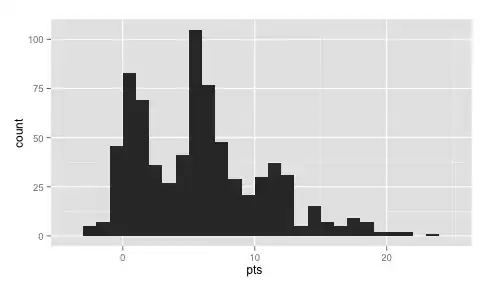
As requested, are are the histograms.
All Players
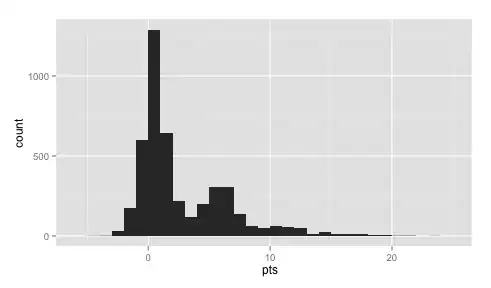
Top 100 Players (based on their avg points)